Three resistors are connected to form the sides of a triangle ABC, the resistance of the sides AB, BC and CA are 40 ohms, 60 ohms and 100 ohms respectively. The effective resistance between the points A and B in ohms will be 

(1) 32

(2) 64

(3) 50

(4) 200

Equivalent resistance across terminals \(A\) and \(B\) will be:

Two wires of the same dimensions but resistivities ρ₁ and ρ₂ are connected in series. The equivalent resistivity of the combination is 

(1) ρ₁ + ρ₂

(2) $\frac{{\rho }_1+{\rho }_2}{2}$

(3) $\sqrt{{\rho }_1{\rho }_2}$

(4) $2({\rho }_1+{\rho }_2)$

A 3 volt battery with negligible internal resistance is connected in a circuit as shown in the figure. The current I, in the circuit will be 

(1) 1/3 A

(2) 1 A

(3) 1.5 A

(4) 2 A

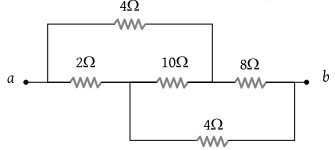
Find the equivalent resistance between the points a and b 

(1) 2 Ω

(2) 4 Ω

(3) 8 Ω

(4) 16 Ω

The potential difference between points A and B is:

         
1. 207 V
2. 407 V
3. 107 V
4. 0

In the circuit shown below, The reading of the voltmeter V is 

(1) 12 V

(2) 8 V

(3) 20 V

(4) 16 V

In the figure given the value of X resistance will be, when the p.d. between B and D is zero 

(1) 4 ohm

(2) 6 ohm

(3) 8 ohm

(4) 9 ohm

Five resistors of given values are connected together as shown in the figure. The current in the arm BD will be 

(1) Half the current in the arm ABC

(2) Zero

(3) Twice the current in the arm ABC

(4) Four times the current in the arm ABC

In the network shown in the figure, each of the resistance is equal to 2 Ω. The resistance between the points A and B is 

(1) 1 Ω

(2) 4 Ω

(3) 3 Ω

(4) 2 Ω