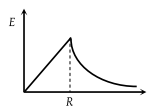
Which of the following graphs shows the variation of electric field E due to a hollow spherical conductor of radius R as a function of distance from the centre of the sphere 

1.		2.
3.		4.

(1)
(2)

(3)
(4)

The electric field due to a uniformly charged solid sphere of radius R as a function of the distance from its centre is represented graphically by -

(1)  (2)

(3)  (4)

Two concentric conducting thin spherical shells \(A\) and \(B\) having radii \(r_A\) and \(r_B\) \((r_B>r_A)\) are charged to \(Q_A\) and $$\(-Q_B~(|Q_B|>|Q_A|).\) The electrical field at distance \(x\) from the common center is:

1.		2.
3.		4.

The electric field inside a spherical shell of uniform surface charge density is -

(1) Zero

(2) Constant, less than zero

(3) Directly proportional to the distance from the centre

(4) None of the above

The distance between charges 5 × 10^–11 C and –2.7 × 10^–11 C is 0.2 m. The distance at which a third charge should be placed in order that it will not experience any force along the line joining the two charges is 

(1) 0.44 m

(2) 0.65 m

(3) 0.556 m

(4) 0.350 m

Suppose the charge of a proton and an electron differ slightly. One of them is \(\text- e\) and the other is \((e+\Delta e)\). If the net of electrostatic force and gravitational force between two hydrogen atoms placed at a distance \(d\) (much greater than atomic size) apart is zero, then $$\(\Delta e\) is of the order: [Given the mass of hydrogen, ${}_{}$\(m_h = 1.67\times 10^{-27}~\text{kg}\)]
1. \(10^{-20}~\text{C}\)
2. \(10^{-23}~\text{C}\)
3. \(10^{-37}~\text{C}\)
4. \(10^{-47}~\text{C}\)

Two identical charged spheres suspended from a common point by two massless strings of lengths l are initially at a distance d(d < < l) apart because of their mutual repulsion. The charges begin to leak from both the spheres at a constant rate. As a result, the spheres approach each other with a velocity v. Then, v varies as a function of the distance x between the sphere, as:

(a) \(v \propto x\)

(b) \(v \propto x^{\frac{-1}{2}}\)

(c) \(v \propto x^{-1}\)

(d) \(v \propto x^{\frac{1}{2}}\)${\frac{\mathrm{}}{}}^{}$
 

The electric field in a certain region is acting radially outward and is given by E=Ar. A charge contained in a sphere of radius 'a' centered at the origin of the field will be given by

1. $4\pi {\in }_{o}A{a}^2$

2. $\pi {\in }_{o}A{a}^2$

3. $4\pi {\in }_{o}A{a}^3$

4. ${\in }_{o}A{a}^2$

Two pith balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is r. Now the strings are rigidly clamped at half the height. The equilibrium separation between the balls now become:

1. (1/√2)²

2. $(r/\sqrt[3]{2})$

3. (2r/√3)

4. (2r/3)

What is the flux through a cube of side 'a' if a point charge q is at one of its corners?

1. $\frac{2q}{{\epsilon }_0}$                                         

2. $\frac{q}{8{\epsilon }_0}$

3. $\frac{q}{{\epsilon }_0}$                                         

4. $\frac{q}{2{\epsilon }_0}6a^2$