A force \(F = -k(y\hat i +x\hat j)\) (where \(k\) is a positive constant) acts on a particle moving in the \(xy\text-\)plane. Starting from the origin, the particle is taken along the positive \(x\text-\)axis to the point \((a,0)\) and then parallel to the \(y\text-\)axis to the point \((a,a)\). The total work done by the force on the particle is:
1. \(-2ka^2\)
2. \(2ka^2\)
3. \(-ka^2\)
4. \(ka^2\)
1. \(-2ka^2\)
2. \(2ka^2\)
3. \(-ka^2\)
4. \(ka^2\)
A lorry and a car moving with the same K.E. are brought to rest by applying the same retarding force, then:
1. Lorry will come to rest in a shorter distance
2. Car will come to rest in a shorter distance
3. Both will come to rest in a same distance
4. None of the above
A particle free to move along the x-axis has potential energy given by for , where k is a positive constant of appropriate dimensions. Then
(1) At point away from the origin, the particle is in unstable equilibrium
(2) For any finite non-zero value of x, there is a force directed away from the origin
(3) If its total mechanical energy is k/2, it has its minimum kinetic energy at the origin
(4) For small displacements from x = 0, the motion is simple harmonic
The kinetic energy acquired by a mass m in travelling a certain distance d starting from rest under the action of a constant force is directly proportional to
(1)
(2) Independent of m
(3)
(4) m
An open knife edge of mass 'm' is dropped from a height 'h' on a wooden floor. If the blade penetrates upto the depth 'd' into the wood, the average resistance offered by the wood to the knife edge is
(1) mg
(2)
(3)
(4)
A body is moving along a straight line by a machine delivering constant power. The distance moved by the body in time t is proportional to
(1) t1/2
(2) t3/4
(3) t3/2
(4) t2
Two particles of masses m1 and m2 in projectile motion have velocities and respectively at time t = 0. They collide at time t0. Their velocities become and at time 2t0 while still moving in air. The value of is
1. Zero
2.
3.
4.
Consider elastic collision of a particle of mass m moving with a velocity u with another particle of the same mass at rest. After the collision the projectile and the struck particle move in directions making angles θ1 and θ2 respectively with the initial direction of motion. The sum of the angles. θ1 + θ2, is
(1) 45°
(2) 90°
(3) 135°
(4) 180°
The relationship between force and position is shown in the given figure (in a one-dimensional case). The work done by the force in displacing a body from \(x = 1~\text{cm}\) to \(x = 5~\text{cm}\) is:

1. \(20~\text{ergs}\)
2. \(60~\text{ergs}\)
3. \(70~\text{ergs}\)
4. \(700~\text{ergs}\)
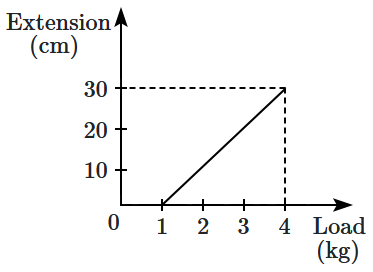
1. \(0.1\text{ N/cm}\)
2. \(5\text{ N/cm}\)
3. \(0.3\text{ N/cm}\)
4. \(1\text{ N/cm}\)






