Figure shows the F-x graph. Where F is the force applied and x is the distance covered by the body along a straight line path. Given that F is in newton and x in metre, what is the work done ?

1. 10 J
2. 20 J
3. 30 J
4. 40 J

The force required to stretch a spring varies with the distance as shown in the figure. If the experiment is performed with the above spring of half length, the line OA will
1. Shift towards F-axis
2. Shift towards X-axis
3. Remain as it is
4. Become double in length
The graph between \(E\) and \(v\) is:
| 1. |  |
2. |  |
| 3. | 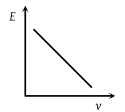 |
4. |  |
A body moves from rest with a constant acceleration. Which one of the following graphs represents the variation of its kinetic energy K with the distance travelled x ?
1.
2.
3.
4.
The diagrams represent the potential energy U as a function of the inter-atomic distance r. Which diagram corresponds to stable molecules found in nature.
1.
2.
3.
4.
The relationship between the force F and the position x of a body is as shown in the figure. The work done in displacing the body from x = 1 m to x = 5 m will be:
| 1. | 30 J | 2. | 15 J |
| 3. | 25 J | 4. | 20 J |
A particle is placed at the origin and a force F = kx is acting on it (where k is positive constant). If U(0) = 0, the graph of U(x) versus x will be (where U is the potential energy function)
1.
2.
3.
4.
Two identical balls \(\mathrm{A}\) and \(\mathrm{B}\) having velocities of \(0.5~\text{m/s}\) and \(-0.3~\text{m/s}\) respectively collide elastically in one dimension. The velocities of \(\mathrm{B}\) and \(\mathrm{A}\) after the collision respectively will be:
1. \(-0.5 ~\text{m/s}~\text{and}~0.3~\text{m/s}\)
2. \(0.5 ~\text{m/s}~\text{and}~-0.3~\text{m/s}\)
3. \(-0.3 ~\text{m/s}~\text{and}~0.5~\text{m/s}\)
4. \(0.3 ~\text{m/s}~\text{and}~0.5~\text{m/s}\)
A body of mass 1 kg begins to move under the action of a time dependent force \(F = 2 t\) \(\hat{i} + 3 t^{2}\ \hat{j}\) N, where \(\hat{i}\) and \(\hat{j}\) are unit vectors along X and Y axis, What power will be developed by the force at the time (t) ?
1. \(\left(2 t^{2} + 4 t^{4}\right) W\)
2. \(\left(2 t^{3} + 3 t^{4}\right) W\)
3. \(\left(2 t^{3} + 3 t^{5}\right) W\)
4. \(\left(2 t + 3 t^{3}\right) W\)
What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
1.
2.
3.
4.




















