A square metallic wire loop of side \(0.1~\text m\) and resistance of \(1~\Omega\) is moved with a constant velocity in a magnetic field of \(2~\text{wb/m}^2\) as shown in the figure. The magnetic field is perpendicular to the plane of the loop and the loop is connected to a network of resistances. What should be the velocity of the loop so as to have a steady current of \(1~\text{mA}\) in the loop?

1. \(1~\text{cm/s}\)
2. \(2~\text{cm/s}\)
3. \(3~\text{cm/s}\)
4. \(4~\text{cm/s}\)

1. \(1~\text{cm/s}\)
2. \(2~\text{cm/s}\)
3. \(3~\text{cm/s}\)
4. \(4~\text{cm/s}\)
A conducting rod PQ of length L = 1.0 m is moving with a uniform speed v = 2 m/s in a uniform magnetic field B = 4.0 T directed into the paper. A capacitor of capacity C = 10 μF is connected as shown in figure. Then
1. qA = + 80 μC and qB = – 80 μC
2. qA = – 80 μC and qB = + 80 μC
3. qA = 0 = qB
4. Charge stored in the capacitor increases exponentially with time
A rectangular loop with a sliding connector of length \(l= 1.0\) m is situated in a uniform magnetic field \(B = 2T\) perpendicular to the plane of the loop. Resistance of connector is \(r=2~\Omega\). Two resistances of \(6~\Omega\) and \(3~\Omega\) are connected as shown in the figure. The external force required to keep the connector moving with a constant velocity \(v = 2\) m/s is:

1. \(6~\text{N}\)
2. \(4~\text{N}\)
3. \(2~\text{N}\)
4. \(1~\text{N}\)
A wire cd of length l and mass m is sliding without friction on conducting rails ax and by as shown. The vertical rails are connected to each other with a resistance R between a and b. A uniform magnetic field B is applied perpendicular to the plane abcd such that cd moves with a constant velocity of
1.
2.
3.
4.
A conducting rod AC of length 4l is rotated about a point O in a uniform magnetic field directed into the paper. AO = l and OC = 3l. Then
1.
2.
3.
4.
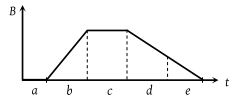
The graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conducting loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first
1. b > (d = e) < (a = c)
2. b > (d = e) > (a = c)
3. b < d < e < c < a
4. b > (a = c) > (d = e)
A rectangular loop is being pulled at a constant speed v, through a region of certain thickness d, in which a uniform magnetic field B is set up. The graph between position x of the right-hand edge of the loop and the induced emf E will be-
1. 
3. 
A flexible wire bent in the form of a circle is placed in a uniform magnetic field perpendicular to the plane of the coil. The radius of the coil changes as shown in the figure. The graph of induced emf in the coil is represented by
1.
2.
3.
4.
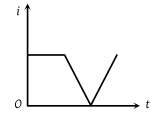
The current i in an induction coil varies with time t according to the graph shown in figure. Which of the following graphs shows the induced emf (e) in the coil with time
1. 
3. 
An electron moves on a straight-line path \(XY\) as shown. The \(abcd\) is a coil adjacent to the path of the electron. What will be the direction of the current, if any induced in the coil?

| 1. | \(abcd\) |
| 2. | \(adcb\) |
| 3. | The current will reverse its direction as the electron goes past the coil. |
| 4. | No current is induced. |