An ac source of angular frequency \(\omega\) is fed across a resistor \(r\) and a capacitor \(C\) in series.
\(I\) is the current in the circuit. If the frequency of the source is changed to \(\frac{\omega}{3}\) (but maintaining the same voltage), the current in the circuit is found to be halved. Calculate the ratio of reactance to resistance at the original frequency \(\omega\).
1.
\(\sqrt{\dfrac{3}{5}}\)
2.
\(\sqrt{\dfrac{2}{5}}\)
3.
\(\sqrt{\dfrac{1}{5}}\)
4.
\(\sqrt{\dfrac{4}{5}}\)
| 1. | \(\frac{\sqrt{5} R}{2} ,\tan^{- 1} \left(2\right)\) | 2. | \(\frac{\sqrt{5} R}{2} , \tan^{- 1} \left(\frac{1}{2}\right)\) |
| 3. | \(\sqrt{5} X_{C} ,\tan^{- 1} \left(2\right)\) | 4. | \(\sqrt{5} R , \tan^{- 1} \left(\frac{1}{2}\right)\) |
In the adjoining ac circuit the voltmeter whose reading will be zero at resonance is
1. V1
2. V2
3. V3
4. V4
In the adjoining figure, the impedance of the circuit will be:
(1) 120 ohm
(2) 50 ohm
(3) 60 ohm
(4) 90 ohm
In a series \(LCR\) circuit, which one of the following curves represents the variation of impedance \((Z)\) with frequency \((f)\)?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
The variation of the instantaneous current \((I)\) and the instantaneous emf \((E)\) in a circuit are shown in the figure. Which of the following statements is correct?

| 1. | The voltage lags behind the current by \(\frac{\pi}{2}\). |
| 2. | The voltage leads the current by \(\frac{\pi}{2}\). |
| 3. | The voltage and the current are in phase. |
| 4. | The voltage leads the current by \(\pi\). |
The figure shows the variation of R, XL, and XC with frequency f in a series L, C, R circuit. Then for what frequency point, the circuit is inductive:
1. A
2. B
3. C
4. All points
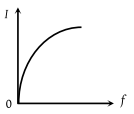
An ac source of variable frequency f is connected to an LCR series circuit. Which one of the graphs in the figure represents the variation of the current I in the circuit with frequency f :
1.
2.
3.
4.
A constant voltage at different frequencies is applied across a capacitance \(C\) as shown in the figure.

Which of the following graphs accurately illustrates how current varies with frequency?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
The output current versus time curve of a rectifier is shown in the figure. The average value of the output current in this case will be:

1. \(0\)
2. \(\dfrac{I_0}{2}\)
3. \(\dfrac{2I_0 }{ \pi}\)
4. \(I_0\)