A bullet of mass 2 gm is having a charge of 2 μC. Through what potential difference must it be accelerated, starting from rest, to acquire a speed of 10 m/s ?

(1) 5 kV

(2) 50 kV

(3) 5 V

(4) 50 V

Figure shows three points A, B and C in a region of uniform electric field $\overrightarrow{E}$. The line AB is perpendicular and BC is parallel to the field lines. Then which of the following holds good. Where $V_A,V_B$ and V_C represent the electric potential at points A, B and C respectively

(1) $V_A=V_B=V_C$

(2) $V_A=V_B>V_C$

(3) $V_A=V_B<V_C$

(4) $V_A>V_B=V_C$

In a certain charge distribution, all points having zero potential can be joined by a circle \(S.\) The points inside \(S\) have positive potential, and points outside \(S\) have a negative potential. A positive charge, which is free to move, is placed inside \(S.\) What is the correct statement about \(S\):

A square of side ‘a’ has charge Q at its centre and charge ‘q’ at one of the corners. The work required to be done in moving the charge ‘q’ from the corner to the diagonally opposite corner is -

(1) Zero

(2) $\frac{Qq}{4\pi {\in }_{0}a}$

(3) $\frac{Qq\sqrt{2}}{4\pi {\in }_{0}a}$

(4) $\frac{Qq}{2\pi {\in }_{0}a}$

As per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge –Q from the point A [co-ordinates (0, a)] to another point B [co-ordinates (a, 0)] along the straight path AB is

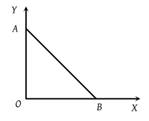
(1) Zero

(2) $\left(\frac{{\displaystyle -qQ}}{{\displaystyle 4\pi {\epsilon }_0}}\frac{{\displaystyle 1}}{{\displaystyle a^2}}\right)\sqrt{2}a$

(3) $\left(\frac{{\displaystyle qQ}}{{\displaystyle 4\pi {\epsilon }_0}}\frac{{\displaystyle 1}}{{\displaystyle a^2}}\right)\frac{a}{\sqrt{2}}$

(4) $\left(\frac{{\displaystyle qQ}}{{\displaystyle 4\pi {\epsilon }_0}}\frac{{\displaystyle 1}}{{\displaystyle a^2}}\right)\sqrt{2}a$

Two charges \(q_1\) and \(q_2\) are placed \(30~\text{cm}\) apart, as shown in the figure. A third charge \(q_3\) is moved along the arc of a circle of radius \(40~\text{cm}\) from \(C\) to \(D.\) The change in the potential energy of the system is \(\dfrac{q_{3}}{4 \pi \varepsilon_{0}} k,\) where \(k\) is:

Two thin wire rings each having a radius R are placed at a distance d apart with their axes coinciding. The charges on the two rings are +q and –q. The potential difference between the centres of the two rings is -

(1) Zero

(2) $\frac{Q}{4\pi {\epsilon }_0}\left[\frac{{\displaystyle 1}}{{\displaystyle R}}-\frac{{\displaystyle 1}}{{\displaystyle \sqrt{R^2+d^2}}}\right]$

(3) $QR/4\pi {\epsilon }_0{d}^2$

(4) $\frac{Q}{2\pi {\epsilon }_0}\left[\frac{{\displaystyle 1}}{{\displaystyle R}}-\frac{{\displaystyle 1}}{{\displaystyle \sqrt{R^2+d^2}}}\right]$

A hollow metallic sphere of radius R is given a charge Q. Then the potential at the centre is -

(1) Zero

(2) $\frac{1}{4\pi {\epsilon }_0}.\frac{Q}{R}$

(3) $\frac{1}{4\pi {\epsilon }_0}.\frac{2Q}{R}$

(4) $\frac{1}{4\pi {\epsilon }_0}.\frac{Q}{2R}$ 

A capacitor is charged by using a battery which is then disconnected. A dielectric slab is then slipped between the plates, which results in -

(1) Reduction of charge on the plates and increase of potential difference across the plates

(2) Increase in the potential difference across the plate, reduction in stored energy, but no change in the charge on the plates

(3) Decrease in the potential difference across the plates, reduction in the stored energy, but no change in the charge on the plates

(4) None of the above

The capacity of a condenser is 4 × 10^–6 farad and its potential is 100 volts. The energy released on discharging it fully will be -

(1) 0.02 Joule

(2) 0.04 Joule

(3) 0.025 Joule

(4) 0.05 Joule