The resultant capacitance across 300 v battery in the figure shown is equal to

1. 1 μF
2. μF
3. 2 μF
4. μF

A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of the resulting system
1. increases by a factor of 4
2.decreases by a factor of 2
3. remain the same
4. increases by a factor of 2
The diagrams below show regions of equipotentials.
| 1. | the maximum work is required to move \(q\) in figure(iii). |
| 2. | in all four cases, the work done is the same. |
| 3. | the minimum work is required to move \(q\) in the figure(i). |
| 4. | the maximum work is required to move \(q\) in figure(ii). |
1. \(8~\text{mC}\)
2. \(2~\text{mC}\)
3. \(5~\text{mC}\)
4. \(7~\mu\text{C}\)
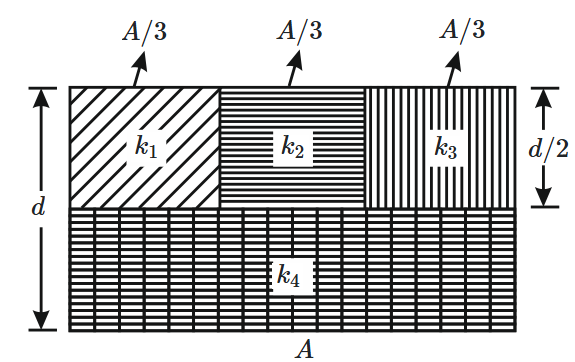
1. \(k = k_{1} + k_{2} + k_{3} + 3 k_{4}\)
3. \(\dfrac{1}{k} = \dfrac{3}{2 \left(k_{1} + k_{2} + k_{3}\right)} + \dfrac{1}{2 k_{4}}\)
4. \(\dfrac{1}{k} = \dfrac{1}{k_{1}} + \dfrac{1}{k_{2}} + \dfrac{1}{k_{3}} + \dfrac{3}{2 k_{4}}\)
A capacitor of \(2~\mu\text{F}\) is charged as shown in the figure. When the switch \(S\) is turned to position \(2\), the percentage of its stored energy dissipated is:

| 1. | \(20\%\) | 2. | \(75\%\) |
| 3. | \(80\%\) | 4. | \(0\%\) |
| 1. | The potential difference between the plates decreases \(K\) times |
| 2. | The energy stored in the capacitor decreases \(K\) times |
| 3. | The change in energy stored is \({1 \over 2} CV^{2}(\frac{1}{K}-1)\) |
| 4. | The charge on the capacitor is not conserved |
If potential (in volts) in a region is expressed as V(x,y,z)=6xy-y+2yz, the electric field (in N/C) at point (1,1,0) is
1. (3+5+3)
2. (6+5+2)
3. (2+3+)
4. (6+9+)
A parallel plate air capacitor has capacity C, distance of separation between plates is d and potential difference V is applied between the plates. Force of attraction between the plates of the parallel plate air capacitor is
1. C2V2/2d
2. CV2/2d
3. CV2/d
4. C2V2/2d2
Two thin dielectric slabs of dielectric constants K1&K2 () are inserted between plates of a parallel capacitor, as shown in the figure. The variation of electric field E between the plates with distance d as measured from plate P is correctly shown by
1.
2.
3.
4.












