An electron, a proton, a deuteron and an alpha particle, each having the same speed are in a region of constant magnetic field perpendicular to the direction of the velocities of the particles. The radius of the circular orbits of these particles are respectively $R_e$, $R_p$, $R_d$ and $R_{\alpha }$. It follows that 

1. $R_e=R_p$               

2. $R_p=R_d$

3. $R_d=R_{\alpha }$                 

4. $R_p=R_{\alpha }$

An infinitely long conductor PQR is bent to form a right angle as shown. A current I flows through PQR. The magnetic field due to this current at the point M is H₁. Now another infinitely long straight conductor QS is connected at Q so that the current is I/2 in QR as well as in QS, The current in PQ remaining unchanged. The magnetic field at M is now $H_{\mathit{2}}$The ratio $H_{\mathit{1}}\mathit{/}{H}_{\mathit{2}}$ is given by

1. $\frac{1}{2}$                                                

2.  1

3.  $\frac{2}{3}$

4.  2

A very long straight wire carries a current I. At the instant when a charge +Qat point P has velocity $\overrightarrow{v}$ , as shown, the force on the charge is:

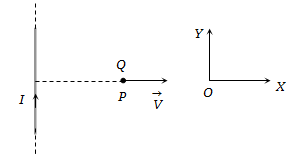
1. Opposite to OX                            
2. Along OX
3. Opposite to OY                             
4. Along OY

An electric field of 1500 V / m and a magnetic field of 0.40 weber / $mete{r}^2$ act on a moving electron. The minimum uniform speed along a straight line the electron could have is

1. $1.6\times {10}^{15}m/s$                         

2. $6\times {10}^{-16}m/s$

3. $3.75\times {10}^{3}m/s$                         

4. $3.75\times {10}^{2}m/s$

A coil having N turns is wound tightly in the form of a spiral with inner and outer radii a and b respectively. When a current I passes through the coil, the magnetic field at the centre is:

1. $\frac{{\mathrm{\mu }}_0\mathrm{NI}}{\mathrm{b}}$                                  2. $\frac{2{\mathrm{\mu }}_0\mathrm{NI}}{\mathrm{a}}$

3. $\frac{{\mathrm{\mu }}_0\mathrm{NI}}{2(\mathrm{b}-\mathrm{a})}\ln \frac{\mathrm{b}}{\mathrm{a}}$                         4. $\frac{{\mathrm{\mu }}_0{\mathrm{I}}^{\mathrm{N}}}{2(\mathrm{b}-\mathrm{a})}\ln \frac{\mathrm{b}}{\mathrm{a}}$

An electron, moving in a uniform magnetic field of induction of intensity $\stackrel{\rightharpoonup }{B,}$ has its radius directly proportional to :

1. Its charge                       

2. Magnetic field

3. Speed                               

4. None of these

A non-planar loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop is of length 2a. The magnetic field due to this loop at the point P (a,0,a) points in the direction

1.  $\frac{1}{\sqrt{2}}\left(-\hat{\mathrm{j}}+\hat{\mathrm{k}}\right)$                                   

2. $\frac{1}{\sqrt{3}}(\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}})$

3.  $\frac{1}{\sqrt{3}}(-\hat{\mathrm{j}}+\hat{\mathrm{k}}+\hat{\mathrm{i}})$                             

4.  $\frac{1}{\sqrt{2}}(\hat{\mathrm{i}}+\hat{\mathrm{k}})$                        

A particle of charge \(q\) and mass \(m\) is moving along the \(x\text-\)axis with a velocity of \(v\) and enters a region of electric field \(E\) and magnetic field \(\mathrm B\) as shown in the figure below. For which figure is the net force on the charge zero?

1.		2.
3.		4.

A current-carrying wire is placed in a uniform magnetic field in the shape of the curve \(y= \alpha \sin \left({\pi x \over L}\right),~0 \le x \le2L.\) $$
What will be the force acting on the wire?