Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time $t_1$. On other days, if she remains stationary on the moving escalator, then the escalator takes her up in time $t_2$. The time taken by her to walk up on the moving escalator will be 

1. $\frac{t_1-t_2}{2}$

2. $\frac{t_1{t}_2}{t_2-t_1}$

3. $\frac{t_1{t}_2}{t_2+t_1}$

4. $t_1-t_2$

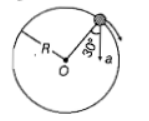
In the given figure, $a=15 m/s^2$ represents the total acceleration of a particle moving in the clockwise direction in a circle of radius R=2.5 m at a given instant of time. The speed of the particle is:

1. 4.5 m/s

2. 5.0 m/s

3. 5.7 m/s 

4. 6.2 m/s

A particle moves so that its position vector is given by \(r=\cos \omega t \hat{x}+\sin \omega t \hat{y}\) where \(\omega\) is a constant. Based on the information given, which of the following is true?

A particle of mass 10g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration, if the kinetic energy of the particle becomes equal to 8x10^-4 J by the end of the second revolution after the beginning of the motion?

(1) 0.15 m/s²

(2) 0.18 m/s²

(3) 0.2 m/s²

(4) 0.1 m/s²

A ship A is moving Westwards with a speed of 10 km h^-1 and a ship B 100 km South of A, is moving Northwards with a speed of 10 km h^-1. The time after which the distance between them becomes shortest is

1., h
2. 5h
3. 5$\sqrt{2}$h
4. 10$\sqrt{2}$h

A projectile is fired from the surface of the earth with a velocity of 5 m/s and angle $\mathrm{\theta }$ with the horizontal. Another projectile fired from another planet with a velocity of 3 m/s at the same angle follows a trajectory, which is identical to the trajectory of the projectile fired from the earth. The value of the acceleration due to gravity on the planet (in m/s²) is: [Given, g = 9.8 m/s²]

1. 3.5

2. 5.9

3. 16.3

4. 110.8

A particle is moving such that its position coordinates (x, y) are (2m, 3m) at time t = 0, (6m, 7m) at time t = 2s and (13m, 14m) at time t = 5s. Average velocity vector (v_av) from t = 0 to t = 5s is

1. $\frac{1}{5}$(13$\hat{i}$+14$\hat{j}$)

2. $\frac{7}{3}$($\hat{i}$+$\hat{j}$)

3. 2($\hat{i}$+$\hat{j}$)

4. $\frac{11}{5}$($\hat{i}$+$\hat{j}$)

The velocity of a projectile at the initial point A is (2i + 3j) m/s. Its velocity (in m/s) at point B is:


1.  -2i+3j

2.  -2i-3j

3.   2i-3j

4.  2i+3j

The horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is:

1. $\theta ={\tan }^{-1}\left(\frac{1}{4}\right)$                                       

2. $\theta ={\tan }^{-1}\left(4\right)$

3. $\theta ={\tan }^{-1}\left(2\right)$                                         

4. $\theta =45°$

A particle has an initial velocity (\(2\hat{i}+3\hat{j}\)) and an acceleration (\(0.3\hat{i}+0.2\hat{j}\)). The magnitude of velocity after \(10\) s will be:
1. \(9 \sqrt{2} ~\text{units} \)
2. \(5 \sqrt{2} ~\text{units} \)
3. \(5 ~\text{units} \)
4. \(9~\text{units} \)