A ring is made of a wire having a resistane 

${\mathrm{R}}_0=12\mathrm{\Omega }$. Find the points A and B, as shown

in the figure, at which a current carrying 

conductor should be connected so that the 

resistance R of the sub circuit between these

points is equal to 8/3$\mathrm{\Omega }$

1. $\frac{{\mathrm{l}}_1}{{\mathrm{l}}_2}=\frac{5}{8}$                    2. $\frac{{\mathrm{l}}_1}{{\mathrm{l}}_2}=\frac{1}{3}$

3. $\frac{{\mathrm{l}}_1}{{\mathrm{l}}_2}=\frac{3}{8}$                    4. $\frac{{\mathrm{l}}_1}{{\mathrm{l}}_2}=\frac{1}{2}$

 

The power dissipated in the circuit shown in

the figure is 30 Watt. The value of R is :

(1) $20\mathrm{\Omega }$

(2) $15\mathrm{\Omega }$

(3) $10\mathrm{\Omega }$

(4) $30\mathrm{\Omega }$

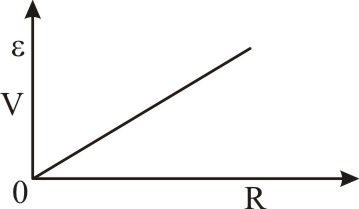
A cell having an emf $\mathrm{\epsilon }$ internal resistance r is connected across a variable external  resistance R. As the resistance R is increased, the plot of potential difference V across R is given by

(a)    

(b) 

(c) 

(d) 

If power dissipated in the 9$\mathrm{\Omega }$ resistor in the circuit shown is 36 W, the potential difference across the 2$\mathrm{\Omega }$ resistor is

1. 8 V
2. 10 V
3. 2 V
4. 4 V

A current of 2A flows through a 2$\mathrm{\Omega }$ resistor

when connected across a battery. The same

battery supplies a current of 0.5 A when

connected across a 9$\mathrm{\Omega }$ resistor. The internal

resistance of the battery is 

(1) $1/3\mathrm{\Omega }$                   

(2) $1/4\mathrm{\Omega }$

(3) $1\mathrm{\Omega }$                       

(4) $0.5\mathrm{\Omega }$

A galvanometer of resistance, G is shunted by a resistance S ohm. To keep the main current in the circuit unchanged, the resistance to be put in series with the galvanometer is

(1) $\frac{S^{\mathit{2}}}{(S+G)}$                                             

(2) $\frac{SG}{(S+G)}$

(3) $\frac{G^{\mathit{2}}}{(S+G)}$                                             

(4) $\frac{G}{(S+G)}$

Which one of the following bonds produces a solid that reflects light in the visible region and whose electrical conductivity decreases with temperature and has high melting point?

(1) metallic bonding

(2) van der Waals'bonding

(3) ionic bonding 

(4) covalent bonding

A potentiometer circuit is set up as shown.The potential gradient across the potentiometer wire, is k volt/cm and the ammeter, present in the circuit, reads 1.0A when two way key is switched off. The balance points, when the key between the terminals (i) 1 and 2 (ii) 1and 3, is plugged in, are found to be at lengths $l_{1}cm and l_{2}cm$ respectively.The magnitudes, of the resistors R and X, in ohm, are then, equal, respectively, to

(a)$k\left(l_2-l_1\right) and k{l}_2$

(b)$k{l}_1 and k\left(l_2-l_1\right)$

(c)$k\left(l_2-l_1\right)and k{l}_1$

(d)$k{l}_1 and k{l}_2$

A galvanometer has a coil of resistance $100\Omega$ and gives a full scale deflection for 30 mA current.If it is to work as a voltmeter of 30V range, the resistance required to be added will be 

(1) 900 $\Omega$                                     

(2) 1800 $\Omega$

(3) 500 $\Omega$                                     

(4) 1000 $\Omega$

A series combination of \(n_1\) capacitors, each of value \(C_1\), is charged by a source of potential difference \(4\) V. When another parallel combination of \(n_2\) capacitors, each of value \(C_2\), is charged by a source of potential difference \(V\), it has the same (total) energy stored in it as the first combination has. The value of \(C_2\) in terms of \(C_1\) is:
1. \(\frac{2C_1}{n_1n_2}\)
2. \(16\frac{n_2}{n_1}C_1\)
3. \(2\frac{n_2}{n_1}C_1\)
4. \(\frac{16C_1}{n_1n_2}\)