A thin conducting ring of radius R is given a charge +Q. The electric field at the centre O of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on the part ACDB of the ring is

1. 3E along KO
2. E along OK
3. E along KO
4. 3E along OK

There is a uniform electric field of strength \(10^3\) V/m along the y-axis. A body of mass \(1\) g and charge \(10^{-6}\) C is projected into the field from the origin along the positive x-axis with a velocity \(10\) m/s. Its speed in m/s after \(10\) s is (neglect gravitational effects)
1. \(10\)
2. \(5\sqrt{2}\)
3. \(10\sqrt{2}\)
4. \(20\)
The electric field at a distance from the centre of a charged conducting spherical shell of radius R is E. The electric field at a distance from the centre of the sphere is
1. 2.
3. 4.
A solid metallic sphere has a charge . Concentric with this sphere is a conducting spherical shell having charge -Q. The radius of the sphere is a and that of the spherical shell is b(b>a). What is the electric field at a distance R(a<R<b) from the centre?
1.
2.
3.
4.
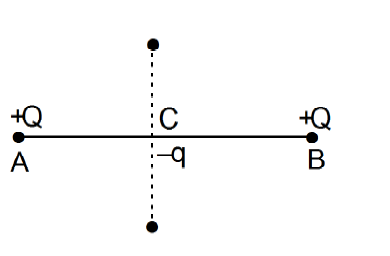
Two similar charge +Q, as shown in figure are placed at A and B. -q charge is placed at point C midway between A and B. -q charge will oscillate if
1. It is moved towards A
2. It is moved towards B
3. It is moved perpendicular to AB
4. Distance between A and B is reduced.
Six charges are placed at the corner of a regular hexagon as shown. If an electron is placed at its centre O, force on it will be:
1. Zero
2. Along OF
3. Along OC
4. None of these
The electric field due to a uniformly charged solid sphere of radius R as a function of the distance from its centre is represented graphically by -
(1) 
(3) 
Four charges equal to – Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is
1.
2.
3.
4.
Two-point charges \(+q\) and \(–q\) are held fixed at \((–d, 0)\) and \((d, 0)\) respectively of a \((x, y)\) coordinate system. Then:
| 1. | \(E\) at all points on the \(y\text-\)axis is along \(\hat i\) |
| 2. | The electric field \(\vec E \) at all points on the \(x\text-\)axis has the same direction |
| 3. | The dipole moment is \(2qd\) directed along \(\hat i\) |
| 4. | The work has to be done to bring a test charge from infinity to the origin |
An infinite number of electric charges each equal to \(5\) nC (magnitude) are placed along the \(x\text-\)axis at \(x=1\) cm, \(x=2\) cm, \(x=4\) cm, \(x=8\) cm ………. and so on. In the setup if the consecutive charges have opposite sign, then the electric field in Newton/Coulomb at \(x=0\) is: \(\left(\frac{1}{4 \pi \varepsilon_{0}} = 9 \times10^{9} ~\text{N-m}^{2}/\text{C}^{2}\right)\)
1. \(12\times 10^{4}\)
2. \(24\times 10^{4}\)
3. \(36\times 10^{4}\)
4. \(48\times 10^{4}\)