On a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K, the period of oscillation of the body (assuming the springs as massless) is

(a) $2\mathrm{\pi }{\left(\frac{M}{2K}\right)}^{1/2}$           (b) $2\mathrm{\pi }{\left(\frac{2\mathrm{M}}{K}\right)}^{1/2}$

(c) $2\mathrm{\pi }\frac{\mathrm{Mg} \mathrm{sin\theta }}{2\mathrm{K}}$           (d) $2\mathrm{\pi }{\left(\frac{2\mathrm{Mg}}{\mathrm{K}}\right)}^{1/2}$

                

A particle of mass m is attached to a spring (of spring constant k) and has a natural angular frequency ${\omega }_0$. An external force F (t) proportional to $\cos \omega t\left(\omega \ne {\omega }_0\right)$ is applied to the oscillator. The time displacement of the oscillator will be proportional to -

(a) $\frac{m}{{{\omega }^2}_0-{\omega }^2}$                 (b) $\frac{1}{m\left({{\omega }^2}_0-{\omega }^2\right)}$

(c) $\frac{1}{m\left({{\omega }^2}_1+{\omega }^2\right)}$            (d) $\frac{m}{{{\omega }^2}_1+{\omega }^2}$

An ideal spring with spring-constant K is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is -

(1) 4 Mg/K         

(2) 2 Mg/K

(3) Mg/K             

(4) Mg/2K

The displacement y of a particle executing periodic motion is given by $y=4{\cos }^2\left(t/2\right)\sin \left(1000t\right).$ This expression may be considered to be a result of the superposition of  ........... independent harmonic motions

1. Two         

2. Three

3. Four         

4. Five

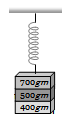
Three masses 700g, 500g, and 400g are suspended at the end of a spring as shown and are in equilibrium. When the 700g mass is removed, the system oscillates with a period of 3 seconds. When the 500 gm mass is also removed, it will oscillate with a period of

1. 1 s

2. 2 s

3. 3 s

4. $\sqrt{\frac{12}{5}}s$

A particle of mass m is attached to three identical springs A, B and C each of force constant k a shown in figure. If the particle of mass m is pushed slightly against the spring A and released then the time period of oscillations is -

(a) $2\mathrm{\pi }\sqrt{\frac{2\mathrm{m}}{\mathrm{k}}}$          (b) $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{2\mathrm{k}}}$

(c) $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$            (d) $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{3\mathrm{k}}}$

The graph shows the variation of displacement of a particle executing SHM with time. We infer from this graph that:

A particle of mass m oscillates with simple harmonic motion between points $x_1$ and $x_2$ , the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph 

1.              

2. 

3.              

4.  

For a particle executing SHM the displacement \(x \) is given by, \(A\cos \omega t.\)  Identify the graph which represents the variation of potential energy (P.E.) as a function of time \(t\) and displacement \(x.\)

   
1. I, III
2. II, IV
3. II, III
4. I, IV

The velocity-time diagram of a harmonic oscillator is shown in the adjoining figure. The frequency of oscillation is

(1) 25 Hz           

(2) 50 Hz

(3) 12.25 Hz       

(4) 33.3 Hz