Consider the situation shown in the figure. The capacitor \(A\) has a charge \(q\) on it whereas \(B\) is uncharged. The charge appearing on the capacitor \(B\) a long time after the switch is closed is: 

1. zero
2. \(\frac{q}{2}\)
3. \(q\)
4. \(2q\)

A capacitor of capacitance C₁ = 1 μF can withstand maximum voltage V₁ = 6kV (kilo-volt) and another capacitor of capacitance C₂ = 3 μF can withstand maximum voltage V₂ = 4 kV. When the two capacitors are connected in series, the combined system can withstand a maximum voltage of

(1) 4 kV

(2) 6 kV

(3) 8 kV

(4) 10 kV

The plates of a parallel plate condenser are pulled apart with a velocity v. If at any instant their mutual distance of separation is d, then the magnitude of the time rate of change of capacity depends on d as follows 

(1) 1/d

(2) 1/d²

(3) d²

(4) d

A fully charged capacitor has a capacitance ‘C’. It is discharged through a small coil of resistance wire embedded in a thermally insulated block of specific heat capacity ‘s’ and mass ‘m’. If the temperature of the block is raised by ‘ΔT’, the potential difference ‘V’ across the capacitance is 

(1) $\frac{ms\Delta T}{C}$

(2) $\sqrt{\frac{2ms\Delta T}{C}}$

(3) $\sqrt{\frac{2mC\Delta T}{s}}$

(4) $\frac{mC\Delta T}{s}$

A network of four capacitors of capacity equal to $C_1=C,C_2=2C,C_3=3C$ and C₄ = 4 C are connected in a battery as shown in the figure. The ratio of the charges on C₂ and C₄ is 

(1) $\frac{22}{3}$

(2) $\frac{3}{22}$

(3) $\frac{7}{4}$

(4) $\frac{4}{7}$

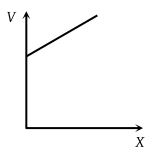
The variation of potential with distance R from a fixed point is as shown below. The electric field at R = 5 m is 

(1) 2.5 volt/m

(2) –2.5 volt/m

(3) 2/5 volt/m

(4) –2/5 volt/m

The figure gives the electric potential V as a function of distance through five regions on x-axis. Which of the following is true for the electric field E in these regions 

(1) $E_1>E_2>E_3>E_4>E_5$

(2) $E_1=E_3=E_5$ and $E_2<E_4$

(3) $E_2=E_4=E_5$ and $E_1<E_3$

(4) $E_1<E_2<E_3<E_4<E_5$

In a hollow spherical shell potential (V) changes with respect to distance (r) from centre 

(1)

(2)

(3)

(4)

What physical quantities may X and Y represent ? (Y represents the first mentioned quantity) 

(1) Pressure v/s temperature of a given gas (constant volume)

(2) Kinetic energy v/s velocity of a particle

(3) Capacitance v/s charge to give a constant potential

(4) Potential v/s capacitance to give a constant charge

Between the plates of a parallel plate capacitor a dielectric plate is introduced just to fill the space between the plates. The capacitor is charged and later disconnected from the battery. The dielectric plate is slowly drawn out of the capacitor parallel to the plates. The plot of the potential difference across the plates and the length of the dielectric plate drawn out is

(1)

(2)

(3)

(4)