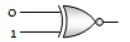
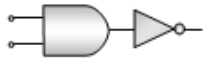
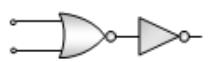
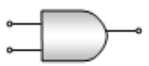
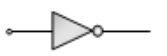
The following truth table corresponds to the logic gate

A  0  0  1  1
B  0  1  0  1
X  0  1  1  1

(1) NAND                     

(2) OR

(3) AND                       

(4) XOR

The combination of ‘NAND’ gates shown here under (figure) are equivalent to

1. An OR gate and an AND gate respectively
2. An AND gate and a NOT gate respectively
3. An AND gate and an OR gate respectively
4. An OR gate and a NOT gate respectively.

A truth table is given below. Which of the following has this type of truth table 

A  0  1  0  1
B  0  0  1  1
y  1  0  0  0

(1) XOR gate

(2) NOR gate

(3) AND gate

(4) OR gate

For the given combination of gates, if the logic states of inputs A, B, C are as follows A = B = C = 0 and A = B = 1, C = 0 then the logic states of output D are

(1) 0, 0

(2) 0, 1

(3) 1, 0

(4) 1, 1

Boolean algebra is essentially based on 

(1) Truth

(2) Logic

(3) Symbol

(4) Numbers

 The logic behind the ‘NOR’ gate is that it gives

(1) High output when both the inputs are low

(2) Low output when both the inputs are low

(3) High output when both the inputs are high

(4) None of these

A logic gate is an electronic circuit which 

(1) Makes logic decisions

(2) Allows electrons flow only in one direction

(3) Works binary algebra

(4) Alternates between 0 and 1 values

A gate has the following truth table 
P 1 1 0 0
Q 1 0 1 0
R 1 0 0 0

The gate is

(1) NOR

(2) OR

(3) NAND

(4) AND

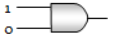
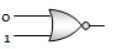
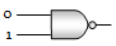
Which of the following gates will have an output of 1

1. 

2. 

3. 

4. 

Which represents NAND gate

1. 

2. 

3. 

4.