The figure shows a system of two concentric spheres of radii \(r_1\) and \(r_2\) and kept at temperatures \(T_1\) and \(T_2,\) respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to: 

                 
1. \(\frac{r_1r_2}{r_1-r_2}\)
2. \(r_1-r_2\)
3. \(({r_1-r_2})({r_1r_2})\)
4. \(\mathrm{ln}\frac{r_2}{r_1}\)

The graph shown in the adjacent diagram, represents the variation of temperature (T) of two bodies, x and y having same surface area, with time (t) due to the emission of radiation. Find the correct relation between the emissivity (e) and absorptivity (a) of the two bodies .

(1) ${\mathrm{e}}_{\mathrm{x}}>{\mathrm{e}}_{\mathrm{y}} \& {\mathrm{a}}_{\mathrm{x}}<{\mathrm{a}}_{\mathrm{y}}$

(2) ${\mathrm{e}}_{\mathrm{x}}<{\mathrm{e}}_{\mathrm{y}} \& {\mathrm{a}}_{\mathrm{x}}>{\mathrm{a}}_{\mathrm{y}}$

(3) ${\mathrm{e}}_{\mathrm{x}}>{\mathrm{e}}_{\mathrm{y}} \& {\mathrm{a}}_{\mathrm{x}}>{\mathrm{a}}_{\mathrm{y}}$

(4) ${\mathrm{e}}_{\mathrm{x}}<{\mathrm{e}}_{\mathrm{y}} \& {\mathrm{a}}_{\mathrm{x}}<{\mathrm{a}}_{\mathrm{y}}$

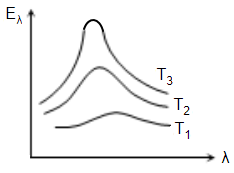
The plots of intensity versus wavelength for three black bodies at temperatures \(T_1, T_2 ~\text{and}~T_3\) respectively are as shown. Their temperature are such that:

1. \(T_1>T_2>T_3\)
2. \(T_1>T_3>T_2\)
3. \(T_2>T_3>T_1\)
4. \(T_3>T_2>T_1\)

The adjoining diagram shows the spectral energy density distribution \(E_{\lambda}\) of a black body at two different temperatures. If the areas under the curves are in the ratio \(16:1,\) the value of temperature \(T\) is: 

  
1. \(32000\) K
2. \(16000\) K
3. \(8000\) K
4. \(4000\) K

Following graph shows the correct variation in intensity of heat radiations by black body and frequency at a fixed temperature

Variation of radiant energy emitted by sun, filament of tungsten lamp and welding arc as a function of its wavelength is shown in figure. Which of the following option is the correct match?

(1) Sun-${\mathrm{T}}_1$, tungsten filament-${\mathrm{T}}_2$ welding arc -${\mathrm{T}}_3$
(2) Sun-${\mathrm{T}}_2$, tungsten filament-${\mathrm{T}}_1$, welding arc- ${\mathrm{T}}_3$
(3) Sun-${\mathrm{T}}_3$, tungsten filament-${\mathrm{T}}_2$ welding arc-${\mathrm{T}}_1$ 
(4) Sun-${\mathrm{T}}_1$, tungsten filament-${\mathrm{T}}_3$, welding arc-${\mathrm{T}}_2$

Shown below are the black body radiation curves at temperatures ${\mathrm{T}}_1$ and ${\mathrm{T}}_2$ (${\mathrm{T}}_2$>${\mathrm{T}}_1$). Which of the following plots is correct ?

The spectrum of a black body at two temperatures 27$°\mathrm{C}$ and 327$°\mathrm{C}$ is shown in the figure. Let ${\mathrm{A}}_1$ and ${\mathrm{A}}_2$ be the areas under the two curves respectively. The value of $\frac{{\mathrm{A}}_2}{{\mathrm{A}}_1}$ is

(a) 1 : 16

(b) 4 : 1

(c) 2 : 1

(d) 16 : 1

A block of metal is heated to a temperature much higher than the room temperature and allowed to cool in a room free from air currents. Which of the following curves correctly represents the rate of cooling?

1.		2.
3.		4.

The energy distribution E with the wavelength $\left(\mathrm{\lambda }\right)$ for the black body radiation at temperature T Kelvin is shown in the figure. As the temperature is increased the maxima will: