An ecosystem which can be easily damaged but can recover after some time if damaging effects stops will be having
1. High stability and low resilience.
2. Low stability and low resilience.
3. High stability and high resilience.
4. Low stability and high resilience.
1. High stability and low resilience.
2. Low stability and low resilience.
3. High stability and high resilience.
4. Low stability and high resilience.
Animals have the innate ability to escape from predation. Select the incorrect example.
1. Color change in chameleon.
2. Poison fangs in snakes.
3. Melanin in moths.
4. Enlargement of body size by swallowing air in puffer fish.
Niche overlap indicates
1. active cooperation between two species.
2. two different parasites on the same host.
3. sharing resources between two species
4. mutualism between two species.
Annual migration does not occur in the case of
1. Salmon
2. Siberian crane.
3. Salamander.
4. arctic tern.
Exponential population growth is represented by
1. dt/dn=rN
2. dN/rN= dt
3. rN/dN= dt
4. dN/dt = rN
Praying mantis is a good example of
1. mullerianmimicary.
2. warning colouration.
3. social insect
4. camouflage.
The population of an insect species shows an explosive increase in number during rainy season followed by its disappearance at the end of the season. What does this show?
| 1. | The population of its predators increases enormously |
| 2. | S-shaped or sigmoid growth of this insect |
| 3. | The food plants mature and die at the end of the rainy season |
| 4. | Its population growth curve is of J-type |
Graph below is a diagrammatic representation of response of organisms to biotic factors. What do a,b,c represent respectively?
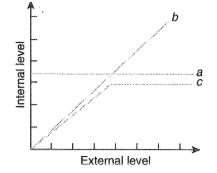
1. Partial regulator, conformer, regulator
2. Regulator, conformer, Partial regulator
3. Conformer, regulator, Partial, regulator
4. Regulator, Partial conformer, regulator
What type of human population is represented by the following age pyramid?
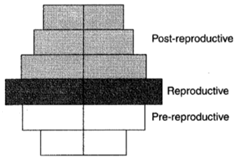
1. Expanding population
2. Vanishing population
3. Stable population
4. Declining population
The logistic population growth is expressed by the equation:
1. \(\dfrac{dN}{dt} = rn \left(\dfrac{N - K}{N}\right)\)
2. \(\dfrac{dt}{dN} = Nr \left(\dfrac{K - N}{K}\right)\)
3. \(\dfrac{dN}{dt} = rN \left(\dfrac{K - N}{K}\right)\)
4. \(\dfrac{dN}{dt} = rN\)






