In the vernier callipers given below, 9 main scale divisions matched with 10 vernier scale divisions. Assume the edge of the vernier scale as the '0' for the vernier scale. The thickness of the object using the defective vernier callipers will be:  
     

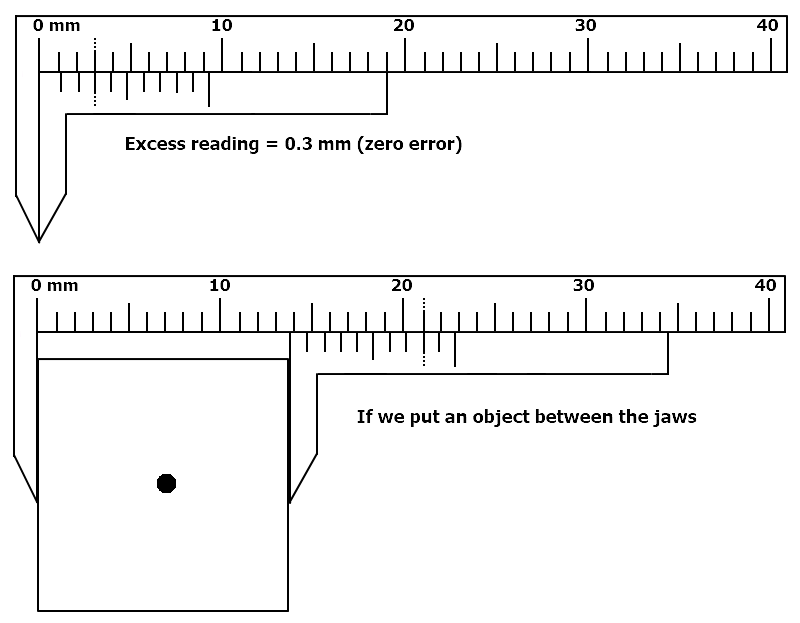
1. 13.3 mm

2. 13.4 mm

3. 13.5 mm

4. 13.6 mm

The main scale of a vernier callipers reads 10 mm in 10 divisions. 10 divisions of Vernier scale coincide with 9 divisions of the main scale. When the two jaws of the callipers touch each other, the fifth division of the vernier coincides with 9 main scale divisions and the zero of the vernier is to the right of zero of main scale. When a cylinder is tightly placed between the two jaws, the zero of vernier scale lies slightly behind 3.2 cm and the fourth vernier division coincides with a main scale division. The diameter of the cylinder is.

(1)  3.10 cm

(2)  3.8 cm

(3)  3.09 cm

(4)  -3.09 cm

The main scale reading is \(-1\) mm when there is no object between the jaws. In the vernier calipers, \(9\) main scale division matches with \(10\) vernier scale divisions. Assume the edge of the Vernier scale as the '\(0\)' of the vernier. The thickness of the object using the defected vernier calipers will be:

         
1. \(12.2~\text{mm}\)
2. \(1.22~\text{mm}\)
3. \(12.3~\text{mm}\)
4. \(12.4~\text{mm}\)

Find the thickness of the wire. The least count is \(0.01~\text{mm}\). The main scale reads (in mm):

                       
1. \(7.62\)
2. \(7.63\)
3. \(7.64\)
4. \(7.65\)

Consider a screw gauge without any zero error. What will be the final reading corresponding to the final state as shown?
It is given that the circular head translates \(P\) MSD in \({N}\) rotations. (\(1\) MSD \(=\) \(1~\text{mm}\).)

              
1. \( \left(\frac{{P}}{{N}}\right)\left(2+\frac{45}{100}\right) \text{mm} \)
2. \( \left(\frac{{N}}{{P}}\right)\left(2+\frac{45}{{N}}\right) \text{mm} \)
3. \(P\left(\frac{2}{{N}}+\frac{45}{100}\right) \text{mm} \)
4. \( \left(2+\frac{45}{100} \times \frac{{P}}{{N}}\right) \text{mm}\)

The pitch of a screw gauge is 1.0 mm and there are 100 divisions on the circular scale. While measuring the diameter of a wire, the linear scale reads 1 mm and the 47^th division on the circular scale coincides with the reference line. The length of the wire is 5.6 cm. Find the wire's curved surface area (in cm²) in an appropriate number of significant figures.

1.  2.4 cm²

2.  2.56 cm²

3.  2.6 cm²

4.  2.8 cm²

The circular division of shown screw gauge are 50. It moves 0.5 mm on main scale in one rotation. The diameter of the ball is 

(1)  2.25 mm

(2)  2.20 mm

(3)  1.20 mm

(4)  1.25 mm

Two full turns of the circular scale of gauge cover a distance of \(1\) mm on scale. The total number of divisions on the circular scale is \(50.\) Further, it is found that screw gauge has a zero error of \(-0.03\) mm. While measuring the diameter of a thin wire a student notes the main scale reading of \(3\) mm and the number of circular scale division in line, with the main scale as \(35.\) The diameter of the wire is:
1. \(3.32\) mm
2. \(3.73\) mm
3. \(3.67\) mm
4. \(3.38\) mm

A Screw Guage gives the following readings when used to measure the diameter of a wire.
Main scale reading = 0.0 mm
Circular scale reading = 52 divisions
Given that: 1 mm on the main scale corresponds to 100 divisions of the circular scale.
The diameter of the wire from the above data is:

1.  0.026 cm

2.  0.005 cm

3.  0.52 cm

4.  0.052 cm