The electrostatic force between the metal plates of an isolated parallel plate capacitor \(C\) having a charge \(Q\) and area \(A\) is:
1.
independent of the distance between the plates.
2.
linearly proportional to the distance between the plates.
3.
proportional to the square root of the distance between the plates.
4.
inversely proportional to the distance between the plates.
A capacitor of \(2~\mu\text{F}\) is charged as shown in the figure. When the switch \({S}\) is turned to position \(2,\) the percentage of its stored energy dissipated is:
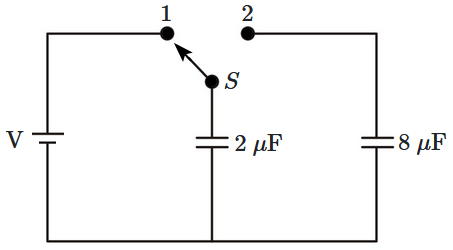
2. \(75\%\)
3. \(80\%\)
4. \(0\%\)
If potential \([\text{in volts}]\) in a region is expressed as \(V[x,y,z] = 6xy-y+2yz,\) the electric field \([\text{in N/C}]\) at point \((1, 1, 0)\) is:
| 1. | \(- \left(3 \hat{i} + 5 \hat{j} + 3 \hat{k}\right)\) | 2. | \(- \left(6 \hat{i} + 5 \hat{j} + 2 \hat{k}\right)\) |
| 3. | \(- \left(2 \hat{i} + 3 \hat{j} + \hat{k}\right)\) | 4. | \(- \left(6 \hat{i} + 9 \hat{j} + \hat{k}\right)\) |
A parallel plate air capacitor has capacitance \(C,\) the distance of separation between plates is \(d\) and potential difference \(V\) is applied between the plates. The force of attraction between the plates of the parallel plate air capacitor is:
| 1. | \(\frac{C^2V^2}{2d}\) | 2. | \(\frac{CV^2}{2d}\) |
| 3. | \(\frac{CV^2}{d}\) | 4. | \(\frac{C^2V^2}{2d^2}\) |
A parallel plate air capacitor of capacitance \(C\) is connected to a cell of emf \(V\) and then disconnected from it. A dielectric slab of dielectric constant \(K,\) which can just fill the air gap of the capacitor is now inserted in it. Which of the following is incorrect?
| 1. | The potential difference between the plates decreases \(K\) times. |
| 2. | The energy stored in the capacitor decreases \(K\) times. |
| 3. | The change in energy stored is \(\frac{1}{2}CV^{2}\left ( \frac{1}{K} -1\right )\) |
| 4. | The charge on the capacitor is not conserved. |
Two thin dielectric slabs of dielectric constants \(K_1\) and \(K_2\) \((K_1<K_2)\) are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field \('E'\) between the plates with distance \('d'\) as measured from the plate \(P\) is correctly shown by:

| 1. |  |
2. |  |
| 3. |  |
4. |  |
A conducting sphere of the radius \(R\) is given a charge \(Q.\) The electric potential and the electric field at the centre of the sphere respectively are:
| 1. | zero and \(\frac{Q}{4 \pi \varepsilon_0 {R}^2}\) | 2. | \(\frac{Q}{4 \pi \varepsilon_0 R}\) and zero |
| 3. | \(\frac{Q}{4 \pi \varepsilon_0 R}\) and \(\frac{Q}{4 \pi \varepsilon_0{R}^2}\) | 4. | both are zero |
In a region, the potential is represented by \(V=(x,y,z)=6x-8xy-8y+6yz,\) where \(V\) is in volts and \(x,y,z\) are in meters. The electric force experienced by a charge of \(2\) coulomb situated at a point \((1,1,1)\) is:
1. \(6\sqrt{5}~\text{N}\)
2. \(30~\text{N}\)
3. \(24~\text{N}\)
4. \(4\sqrt{35}~\text{N}\)
\(A\), \(B\) and \(C\) are three points in a uniform electric field. The electric potential is:

| 1. | maximum at \(B\) |
| 2. | maximum at \(C\) |
| 3. | same at all the three points \(A, B\) and \(C\) |
| 4. | maximum at \(A\) |
Four-point charges \(-Q, -q, 2q~\text{and}~2Q\) are placed, one at each corner of the square. The relation between \(Q\) and \(q\) for which the potential at the center of the square is zero is:
| 1. | \(Q= -q\) | 2. | \(Q= -2q\) |
| 3. | \(Q= q\) | 4. | \(Q= 2q\) |






