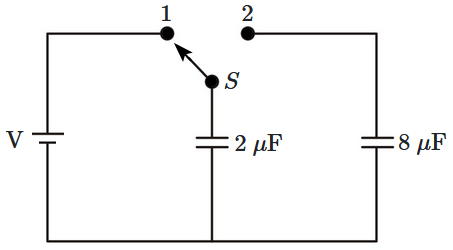
A capacitor of \(2~\mu\text{F}\) is charged as shown in the figure. When the switch \({S}\) is turned to position \(2,\) the percentage of its stored energy dissipated is:
 1. \(20\%\)
1. \(20\%\)
2. \(75\%\)
3. \(80\%\)
4. \(0\%\)

2. \(75\%\)
3. \(80\%\)
4. \(0\%\)
If potential \([\text{in volts}]\) in a region is expressed as \(V[x,y,z] = 6xy-y+2yz,\) the electric field \([\text{in N/C}]\) at point \((1, 1, 0)\) is:
| 1. | \(- \left(3 \hat{i} + 5 \hat{j} + 3 \hat{k}\right)\) | 2. | \(- \left(6 \hat{i} + 5 \hat{j} + 2 \hat{k}\right)\) |
| 3. | \(- \left(2 \hat{i} + 3 \hat{j} + \hat{k}\right)\) | 4. | \(- \left(6 \hat{i} + 9 \hat{j} + \hat{k}\right)\) |
A parallel plate air capacitor has capacitance \(C,\) the distance of separation between plates is \(d\) and potential difference \(V\) is applied between the plates. The force of attraction between the plates of the parallel plate air capacitor is:
| 1. | \(\frac{C^2V^2}{2d}\) | 2. | \(\frac{CV^2}{2d}\) |
| 3. | \(\frac{CV^2}{d}\) | 4. | \(\frac{C^2V^2}{2d^2}\) |
Two thin dielectric slabs of dielectric constants \(K_1\) and \(K_2\) \((K_1<K_2)\) are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field \('E'\) between the plates with distance \('d'\) as measured from the plate \(P\) is correctly shown by:

| 1. |  |
2. |  |
| 3. |  |
4. |  |
In a region, the potential is represented by \(V=(x,y,z)=6x-8xy-8y+6yz,\) where \(V\) is in volts and \(x,y,z\) are in meters. The electric force experienced by a charge of \(2\) coulomb situated at a point \((1,1,1)\) is:
1. \(6\sqrt{5}~\text{N}\)
2. \(30~\text{N}\)
3. \(24~\text{N}\)
4. \(4\sqrt{35}~\text{N}\)
\(A\), \(B\) and \(C\) are three points in a uniform electric field. The electric potential is:

| 1. | maximum at \(B\) |
| 2. | maximum at \(C\) |
| 3. | same at all the three points \(A, B\) and \(C\) |
| 4. | maximum at \(A\) |
An electric dipole of moment \(p\) is placed in an electric field of intensity \(E.\) The dipole acquires a position such that the axis of the dipole makes an angle \(\theta\) with the direction of the field. Assuming that the potential energy of the dipole to be zero when \(\theta = 90^{\circ}\), the torque and the potential energy of the dipole will respectively be:
1. \(pE\text{sin}\theta, ~-pE\text{cos}\theta\)
2. \(pE\text{sin}\theta, ~-2pE\text{cos}\theta\)
3. \(pE\text{sin}\theta, ~2pE\text{cos}\theta\)
4. \(pE\text{cos}\theta, ~-pE\text{sin}\theta\)
Three capacitors each of capacitance \(C\) and of breakdown voltage \(V\) are joined in series. The capacitance and breakdown voltage of the combination will be:
1.
2.
3.
4. \(3C,~3V\)
The electric field at that point is:
2. = 2xy + (x2 +y2) +(3xz-y2)
3. = z3 + xyz + z2
4. = (2xy- z3) + xy2 + 3z2x
The electric potential at a point in free space due to a charge \(Q\) coulomb is \(Q\times10^{11}~\text{V}\). The electric field at that point is:
1. \(4\pi \varepsilon_0 Q\times 10^{22}~\text{V/m}\)
2. \(12\pi \varepsilon_0 Q\times 10^{20}~\text{V/m}\)
3. \(4\pi \varepsilon_0 Q\times 10^{20}~\text{V/m}\)
4. \(12\pi \varepsilon_0 Q\times 10^{22}~\text{V/m}\)






