\(220 ~\mathrm{V}\), \(50~\mathrm{Hz}\), AC source is connected to an inductance of \(0.2~\mathrm{H}\) and a resistance of \(20\) \(\Omega\) in series. What is the current in the circuit?

1. \(3.33~\mathrm{A}\) 
2. \(33.3~\mathrm{A}\) 
3. \(5\mathrm{A}\) 
4. \(10\mathrm{~A}\) 

Voltage across each elements of a series LCR
circuit are given by V_L= 60V, V_C= 20V,V_R= 30V
Find out source voltage.
1. 50V 

2. 100V 

3. 150V 

4. 200V

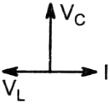
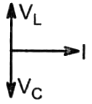
The current I, potential difference V_L across the inductor and potential difference V_C across the capacitor in the circuit as shown in the figure are best represented vectorially as:

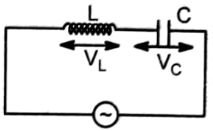
1. 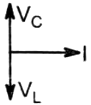                                     2.  

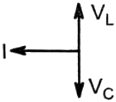3.                                  4.  

Resonance occurs in a series L-C-R circuit when the frequency of the applied e.m.f. is 1000 Hz. Then:

1.  when f=900 Hz, the circuit behaves as a capacitive circuit

2.  the impendence of the circuit is maximum at f=1000 Hz

3.  at resonance the voltages across L and current in C differ in phase by 180$°$

4.  if the value of C is doubled resonance occurs at f=2000 Hz

If we change the value of \(R,\) then:
  

In an AC circuit, the emf (e) and the current (I) at any instant are given respectively by 
e = E₀sin$\mathrm{\omega }$t 
I = I₀sin$\left(\mathrm{\omega t}-\mathrm{\varphi }\right)$ 
The average power in the circuit over one cycle of AC is:

1.  $\frac{{\mathrm{E}}_{\mathrm{o}}{\mathrm{I}}_{\mathrm{o}}}{2}$

2.  $\frac{{\mathrm{E}}_{\mathrm{o}}{\mathrm{I}}_{\mathrm{o}}}{2}$ $\sin$ $\mathrm{\varphi }$

3.  $\frac{{\mathrm{E}}_{\mathrm{o}}{\mathrm{I}}_{\mathrm{o}}}{2}$ $\cos$ $\mathrm{\varphi }$

4.  ${\mathrm{E}}_{\mathrm{o}}{\mathrm{I}}_{\mathrm{o}}$

The power dissipated in an L-C-R series circuit connected to an AC source of emf E is:

In the given circuit, the reading of voltmeter V₁ and V₂ are 300 V each. The reading of the voltmeter V₃ and ammeter A are respectively:

1. 150 V, 2.2 A

2. 220 V, 2.2 A

3. 220 V, 2.0 A

4. 100 V, 2.0 A

An AC voltage is applied to a resistance R and an inductor L in series. If R and the inductive reactance are both equal to 3 $\Omega$, the phase difference between the applied voltage and the current in the circuit is:

1.  $\frac{\mathrm{\pi }}{4}$

2.  $\frac{\mathrm{\pi }}{2}$

3.  zero

4.  $\frac{\mathrm{\pi }}{6}$