Two blocks of 4 kg and 6 kg are attached by springs, they are hanging in vertical position, lower spring breaks due to excessive force. Acceleration of 4 kg block just after breaking

1. 15 $m/s^2$

2. 25 $m/s^2$

3. 10 $m/s^2$

4. Zero

The tension in the spring is

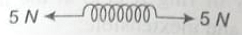
1. Zero

2. 2.5 N

3. 5 N

4. 10 N

A block can slide on a smooth inclined plane of inclination $\theta$ kept on the floor of a lift. When the lift is descending with retardation a, the acceleration of the block relative to the incline is:

1.  (g + a) sin $\mathrm{\theta }$              
2.  (g – a)
3.  g sin $\mathrm{\theta }$
4.  (g – a) sin $\mathrm{\theta }$

In the system shown $m_1>m_2$. System is held at rest by thread BC. Just after lower thread is Burnt.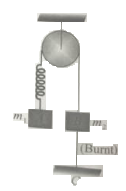

1. Acceleration of $m_2$ is upward

2. Magnitude of acceleration of both blocks will be $\left(\frac{m_1-m_2}{m_1+m_2}\right)g$

3. Acceleration of $m_1$ will be non-zero

4. Magnitude of acceleration of two blocks will be non-zero and unequal.

System shown in figure is in equilibrium and at rest. The spring and string are massless, now the stringis cut. The acceleration of mass 2m and m just after string is cut will be

1. g/2 upwards, g downwards

2. g upwards, g/2 downwards

3. g upwards, 2g downwards

4. 2g upwards, g downwards

The pulleys and string shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle \(\theta\) should be:

      

1. 0°
2. 30$°$
3. 45$°$
4. 60$°$

A pendulum of mass m hangs from a support fixed to a trolley. The direction of the string when the trolley rolls up a plane of inclination $\alpha$ with acceleration $a_0$ is 

1. $\theta ={\tan }^{-1} \alpha$

2. $\theta ={\tan }^{-1} \left(\frac{a_0}{g}\right)$

3. $\theta ={\tan }^{-1} \left(\frac{g}{a_0}\right)$

4. $\theta ={\tan }^{-1} \left(\frac{a_0+g \sin \alpha }{g \cos \alpha }\right)$

A mass m₁, placed on top of a trolley of mass m₃, is connected to another mass m₂ by means of string passing over a smooth pulley as shown in figure. The friction between surfaces is negligible. For m₁ ans m₂ not to move with respect to trolley, the horizontal force F to be applied on trolley is

1. F=m₃g

2. F=(m₁ + m₂)g

3. $\mathrm{F}=\left({\mathrm{m}}_1+{\mathrm{m}}_2+{\mathrm{m}}_3\right)\frac{{\mathrm{m}}_2\mathrm{g}}{{\mathrm{m}}_1}$

4. F= m₁g

In the shown system, each of the blocks is at rest. The value of \(\theta\) is:
 
1. \(\tan^{- 1} \left(1\right)\)
2. \(\tan^{- 1} \left(\frac{3}{4}\right)\)
3. \(\tan^{- 1} \left(\frac{4}{3}\right)\)
4. \(\tan^{- 1} \left(\frac{3}{5}\right)\)

A particle moving with velocity \(\vec{v}\) is acted by three forces shown by the vector triangle \(\mathrm{PQR}.\) The velocity of the particle will: