- 1(current)
Q. No.
| 1. | \(9^\circ\) | 2. | \(10^\circ\) |
| 3. | \(4^\circ\) | 4. | \(6^\circ\) |
Find the value of the angle of emergence from the prism given below for the incidence ray shown. The refractive index of the glass is \(\sqrt{3}\).
1. \(45^{\circ}\)
2. \(90^{\circ}\)
3. \(60^{\circ}\)
4. \(30^{\circ}\)
A ray is incident at an angle of incidence \(i\) on one surface of a small angle prism (with the angle of the prism \(A\)) and emerges normally from the opposite surface. If the refractive index of the material of the prism is \(\mu,\) then the angle of incidence is nearly equal to:
| 1. | \(\dfrac{2A}{\mu}\) | 2. | \(\mu A\) |
| 3. | \(\dfrac{\mu A}{2}\) | 4. | \(\dfrac{A}{2\mu}\) |
The refractive index of the material of a prism is \(\sqrt{2}\) and the angle of the prism is \(30^\circ.\) One of the two refracting surfaces of the prism is made a mirror inwards with a silver coating. A beam of monochromatic light entering the prism from the other face will retrace its path (after reflection from the silvered surface) if the angle of incidence on the prism is:
| 1. | \(60^\circ\) | 2. | \(45^\circ\) |
| 3. | \(30^\circ\) | 4. | zero |
A thin prism having refracting angle \(10^\circ\) is made of glass of a refractive index \(1.42\). This prism is combined with another thin prism of glass with a refractive index \(1.7\). This combination produces dispersion without deviation. The refracting angle of the second prism should be:
1. \(6^{\circ}\)
2. \(8^{\circ}\)
3. \(10^{\circ}\)
4. \(4^{\circ}\)
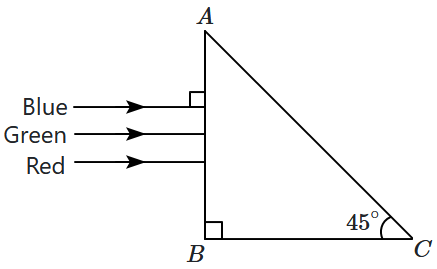
The prism will:
| 1. | separate the blue colour part from the red and green colour. |
| 2. | separate all three colours from one another. |
| 3. | not separate the three colours at all. |
| 4. | separate the red colour part from the green and blue colours. |
The angle of a prism is \(A\). One of its refracting surfaces is silvered. Light rays falling at an angle of incidence \(2{A}\) on the first surface return back through the same path after suffering reflection at the silvered surface. The refractive index \(\mu,\) of the prism, is:
1. \(2\text{sin}A\)
2. \(2\text{cos}A\)
3. \(\dfrac{1}{2}\text{cos}A\)
4. \(\text{tan}A\)
For the angle of minimum deviation of a prism to be equal to its refracting angle, the prism must be made of a material whose refractive index:
| 1. | lies between \(2\) and \(\sqrt{2}\) |
| 2. | is less than \(1\) |
| 3. | is greater than \(2\) |
| 4. | lies between \(\sqrt{2}\) and \(1\) |
1. \(30^\circ\)
2. \(60^\circ\)
3. \(100^\circ\)
4. \(120^\circ\)
| Assertion (A): | There is no dispersion of light refracted through a rectangular glass slab. |
| Reason (R): | Dispersion of light is the phenomenon of splitting of a beam of white light into its constituent colours. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.