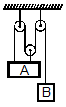
At a given instant, A is moving with velocity of 5 m/s upwards. What is velocity of B at this time?
1. 15 m/s
2. 15 m/s
3. 5 m/s
4. 5 m/s

The blocks \(A\) and \(B\) are shown in figure have masses \(5\) kg and \(4\) kg respectively. The system is released from rest. The speed of \(B\) after \(A\) has travelled a distance \(1\) m along the incline is: (take \(g = 10~\text{m/s}^2\), pulleys and strings are ideal and plane is smooth)
1. \(\sqrt{\frac{6}{5}}~\text{m/s}\)
2. \(\sqrt{\frac{3}{2}}~\text{m/s}\)
3. \(\sqrt{\frac{5}{6}}~\text{m/s}\)
4. \(\sqrt{\frac{2}{3}}~\text{m/s}\)
In the shown system, each of the blocks is at rest. The value of \(\theta\) is:

1. \(\tan^{- 1} \left(1\right)\)
2. \(\tan^{- 1} \left(\frac{3}{4}\right)\)
3. \(\tan^{- 1} \left(\frac{4}{3}\right)\)
4. \(\tan^{- 1} \left(\frac{3}{5}\right)\)
A truck is stationary and has a bob suspended by a light string in a frame attached to the truck. The truck suddenly moves to the right with an acceleration of \(a.\) In the frame of the truck, the pendulum will tilt:
| 1. | to the left and the angle of inclination of the pendulum with the vertical is \(\text{sin}^{-1} \left( \dfrac{a}{g} \right )\) |
| 2. | to the left and the angle of inclination of the pendulum with the vertical is \(\text{cos}^{-1} \left ( \dfrac{a}{g} \right )\) |
| 3. | to the left and the angle of inclination of the pendulum with the vertical is \(\text{tan}^{-1} \left ( \dfrac{a}{g} \right )\) |
| 4. | to the left and the angle of inclination of the pendulum with the vertical is \(\text{tan}^{-1} \left ( \dfrac{g}{a} \right )\) |
A body of mass \(m\) is kept on a rough horizontal surface (coefficient of friction = \(\mu).\) A horizontal force is applied to the body, but it does not move. The resultant of normal reaction and the frictional force acting on the object is given by \(\vec {F}\) where:
1. \(|{\vec {F}}| = mg+\mu mg\)
2. \(|\vec {F}| =\mu mg\)
3. \(|\vec {F}| \le mg\sqrt{1+\mu^2}\)
4. \(|\vec{F}| = mg\)
A block can slide on a smooth inclined plane of inclination kept on the floor of a lift. When the lift is descending with retardation a, the acceleration of the block relative to the incline is:
1. (g + a) sin
2. (g – a)
3. g sin
4. (g – a) sin
Two blocks of 4 kg and 6 kg are attached by springs, they are hanging in vertical position, lower spring breaks due to excessive force. Acceleration of 4 kg block just after breaking
1. 15
2. 25
3. 10
4. Zero
In the system shown . System is held at rest by thread BC. Just after lower thread is Burnt.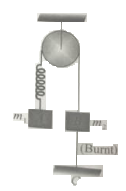
1. Acceleration of is upward
2. Magnitude of acceleration of both blocks will be
3. Acceleration of will be non-zero
4. Magnitude of acceleration of two blocks will be non-zero and unequal.
System shown in figure is in equilibrium and at rest. The spring and string are massless, now the stringis cut. The acceleration of mass 2m and m just after string is cut will be
1. g/2 upwards, g downwards
2. g upwards, g/2 downwards
3. g upwards, 2g downwards
4. 2g upwards, g downwards