A truck is stationary and has a bob suspended by a light string in a frame attached to the truck. The truck suddenly moves to the right with an acceleration of \(a.\) In the frame of the truck, the pendulum will tilt:

1.	to the left and the angle of inclination of the pendulum with the vertical is \(\text{sin}^{-1} \left( \dfrac{a}{g} \right )\)
2.	to the left and the angle of inclination of the pendulum with the vertical is \(\text{cos}^{-1} \left ( \dfrac{a}{g} \right )\)
3.	to the left and the angle of inclination of the pendulum with the vertical is \(\text{tan}^{-1} \left ( \dfrac{a}{g} \right )\)
4.	to the left and the angle of inclination of the pendulum with the vertical is \(\text{tan}^{-1} \left ( \dfrac{g}{a} \right )\)

A body of mass \(m\) is kept on a rough horizontal surface (coefficient of friction = \(\mu).\) A horizontal force is applied to the body, but it does not move. The resultant of normal reaction and the frictional force acting on the object is given by \(\vec {F}\) where:
1. \(|{\vec {F}}| = mg+\mu mg\)
2. \(|\vec {F}| =\mu mg\)
3. \(|\vec {F}| \le mg\sqrt{1+\mu^2}\)
4. \(|\vec{F}| = mg\)

The blocks \(A\) and \(B\) are shown in figure have masses \(5\) kg and \(4\) kg respectively. The system is released from rest. The speed of \(B\) after \(A\) has travelled a distance \(1\) m along the incline is: (take \(g = 10~\text{m/s}^2\), pulleys and strings are ideal and plane is smooth)

 
1. \(\sqrt{\frac{6}{5}}~\text{m/s}\)
2. \(\sqrt{\frac{3}{2}}~\text{m/s}\)
3. \(\sqrt{\frac{5}{6}}~\text{m/s}\)
4. \(\sqrt{\frac{2}{3}}~\text{m/s}\)

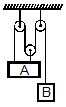
At a given instant, A is moving with velocity of 5 m/s upwards. What is velocity of B at this time?

1. 15 m/s $\downarrow$

2. 15 m/s $\uparrow$

3. 5 m/s $\downarrow$

4. 5 m/s $\uparrow$

In the shown system, each of the blocks is at rest. The value of \(\theta\) is:
 
1. \(\tan^{- 1} \left(1\right)\)
2. \(\tan^{- 1} \left(\frac{3}{4}\right)\)
3. \(\tan^{- 1} \left(\frac{4}{3}\right)\)
4. \(\tan^{- 1} \left(\frac{3}{5}\right)\)

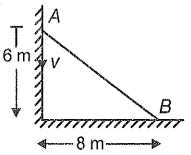
A ladder rests against a smooth vertical wall as shown in the figure. The floor is also smooth. The mass of the ladder is 75 kg. If upper-end A is moving with velocity v vertically downward, then the horizontal velocity of lower end B is :

1.  v

2.  $\frac{3}{4}\mathrm{v}$

3.  $\frac{4}{3}\mathrm{v}$

4.  $\frac{3}{5}\mathrm{v}$

Which of the following sets of concurrent forces may be in equilibrium?

(1) ${\mathrm{F}}_1$ = 2 N, ${\mathrm{F}}_2$ = 5 N, ${\mathrm{F}}_3$ = 9 N

(2) ${\mathrm{F}}_1$ = 3 N, ${\mathrm{F}}_2$ = 6 N, ${\mathrm{F}}_3$ = 8 N

(3) ${\mathrm{F}}_1$ = 4 N, ${\mathrm{F}}_2$ = 6 N, ${\mathrm{F}}_3$ = 12 N

(4) ${\mathrm{F}}_1$ = 5 N, ${\mathrm{F}}_2$ = 10 N, ${\mathrm{F}}_3$ = 4 N

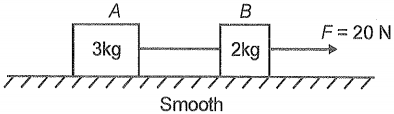
Two blocks A and B are connected by a light string as shown in the figure. The force exerted by the string on the block B is:

1. 20 N

2. 15 N

3. 12 N

4. 8 N

A rod of mass m length l is moving between perpendicular smooth walls as shown. When the rod is at an angle \(\theta\) with horizontal its end \(A\) is moving right with speed \(v\). The speed of end \(B\) is:

               
1. \(v\cot \theta\)
2. \(v\tan \theta\)
3. \(v\cos \theta\)
4. \(v\sin \theta\)

The figure shows a rod of length \(5\) m. Its ends, \(A\) and \(B\), are restrained to moving in horizontal and vertical guides. When the end \(A\) is \(3\) m above \(O\), it moves at \(4\) m/s. The velocity of end \(B\) at that instant is:
                         
1. \(2\) m/s
2. \(3\) m/s
3. \(4\) m/s
4. \(0.20\) m/s