The molar heat capacity C for an ideal gas going through a given process is given by C = a/T , where 'a' is a constant. If  $\mathrm{\gamma }= {\mathrm{C}}_{\mathrm{P}}/{\mathrm{C}}_{\mathrm{V}}$ , the work done by one mole of gas during heating from ${\mathrm{T}}_0$ to $\mathrm{\eta } {\mathrm{T}}_0$ through the given process will be:

1.  $\frac{1}{\mathrm{a}} \ln \mathrm{\eta }$

2.  $\mathrm{a} \ln \mathrm{\eta }- \left(\frac{\mathrm{\eta }-1}{\mathrm{\gamma }-1}\right) {\mathrm{RT}}_0$

3.  $\mathrm{a} \ln \mathrm{\eta }-\left(\mathrm{\gamma }-\mathrm{A}\right) {\mathrm{RT}}_0$

4.  none of these

The pressure of a monoatomic gas increases linearly from $4\times {10}^5$ N/m² to $8\times {10}^5$ N/m² when its volume increases from 0.2 m³ to 0.5 m³. The molar heat capacity of the gas is:
[R = 8.31 J/mol k]  

1. 20.1 J/molK               

2. 17.14 J/molK

3. 18.14 J/molK                                   

4. 20.14 J/molK

An ideal gas expands according to the law ${\mathrm{PV}}^2$ = const. The molar heat capacity C is : 

1. ${\mathrm{C}}_{\mathrm{V}} + \mathrm{R}$ 

2. ${\mathrm{C}}_{\mathrm{V}} – \mathrm{R}$ 

3. ${\mathrm{C}}_{\mathrm{V}} + 2\mathrm{R}$

4. ${\mathrm{C}}_{\mathrm{V}} – 3\mathrm{R}$

The molar heat capacity for an ideal gas

1.  cannot be negative

2.  must be equal to either ${\mathrm{C}}_{\mathrm{V}}$ or ${\mathrm{C}}_{\mathrm{P}}$

3.  must lie in the range ${\mathrm{C}}_{\mathrm{V}}\le \mathrm{C}\le {\mathrm{C}}_{\mathrm{P}}$

4.  may have any value between $-\infty$ and $+\infty$

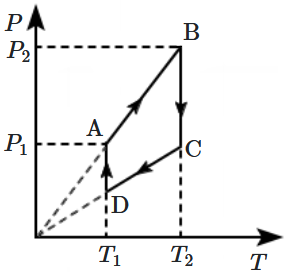
An ideal gas undergoes a cyclic process as shown in the graph between pressure \((P)\) and temperature \((T).\) The part of the graph which represents the absorption of heat from the surrounding are:

Ideal gas is taken through cycle $P\to Q\to R\to P$ as shown in the figure. If net heat supplied to the gas in the cycle is 15 J, the work done by the gas in the process $R\to P$ is

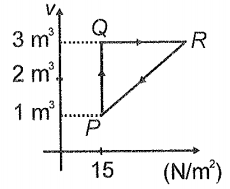
1. 5J

2. -15 J

3. -20 J

4. -12 J

Internal energy remains the same throughout the process along the path in

1 Adiabatic process

2 Isothermal process

3 Cyclic process

4 Both (2) & (3)

The cyclic process of \(2\) moles of diatomic gas is shown in the figure. Which of the following statements is correct?

Without external heat work done possible in

1 Adiabatic process

2 Isochoric process

3 Isothermal process

4 Isobaric process