Heat capacity is equal to the product of:

1.  mass and gas constant

2.  mass and specific heat

3.  latent heat and volume of water

4.  mass and Avogadro number

 

When a block of iron floats in Hg at $0°C$, a fraction $K_1$ of its volumen= is submerged, while at temperature of $60°C$ a fraction $K_2$ is seen to be submersed. If the coefficient of volume expansion of iron is ${\gamma }_{Fe}$ and that of mercury is ${\gamma }_{Hg}$, then the ratio $\frac{K_1}{K_2}$ can be expressed as:

(1) $\frac{1+60{\gamma }_{Fe}}{1+60{\gamma }_{Hg}}$

(2) $\frac{1-60{\gamma }_{Fe}}{1+60{\gamma }_{Hg}}$

(3) $\frac{1+60{\gamma }_{Fe}}{1-60{\gamma }_{Hg}}$

(4) $\frac{1+60{\gamma }_{He}}{1-60{\gamma }_{Fe}}$

$\mathrm{If} {\mathrm{\alpha }}_{\mathrm{c}} \mathrm{and} {\mathrm{\alpha }}_{\mathrm{f}} \mathrm{denote} \mathrm{the} \mathrm{numerical} \mathrm{values} \mathrm{of} \mathrm{coefficient} \mathrm{of} \mathrm{linear}$
$\mathrm{expansion} \mathrm{of} \mathrm{a} \mathrm{solid}, \mathrm{expressed} \mathrm{per} °\mathrm{C} \mathrm{and} \mathrm{per} °\mathrm{F} \mathrm{respectively},$
$\mathrm{then}$

1.  ${\alpha }_c > {\alpha }_f$

2.  ${\alpha }_f > {\alpha }_c$

3.  ${\alpha }_f = {\alpha }_c$

4.  ${\alpha }_f + {\alpha }_c = 0$

$$\begin{gathered} \mathrm{A} \mathrm{pendulum} \mathrm{clock} \mathrm{runs} \mathrm{fast} \mathrm{by} 5 \sec . \mathrm{per} \mathrm{day} \mathrm{at} 20°\mathrm{C} \mathrm{and} \mathrm{goes} \mathrm{slow} \\ \mathrm{by} 10 \sec . \mathrm{per} \mathrm{day} \mathrm{at} 35°\mathrm{C}. \mathrm{It} \mathrm{shows} \mathrm{correct} \mathrm{time} \mathrm{at} \mathrm{a} \mathrm{temperature} \mathrm{of} \end{gathered}$$

1.  $27.5°\mathrm{C}$

2.  $25°\mathrm{C}$

3.  $30°\mathrm{C}$

4.  $33°\mathrm{C}$

Two identical bodies are made of a material whose heat capacity increases with temperature. One of these is at ${\mathrm{}}^{}$\(100^{\circ} \mathrm{C}\), while the other one is at ${\mathrm{}}^{}$\(0^{\circ} \mathrm{C}\). If the two bodies are brought into contact, then assuming no heat loss, the final common temperature will be:

A piece of ice falls from a height h so that it melts completely. Only one-quarter of the heat produced is absorbed by the ice and all energy of ice gets converted into heat during its fall. The value of h is [Latent heat of ice is 3.4x10⁵J/Kg and g=10N/Kg]

1. 544 km

2. 136 km

3.  68  km

4.  34 km

The value of the coefficient of volume expansion of glycerin is \(5\times10^{-4}\) K^-1. The fractional change in the density of glycerin for a temperature increase of \(40^\circ \mathrm{C}\) will be:

Steam at \(100^{\circ}\mathrm{C}\) is injected into 20 g of \(10^{\circ}\mathrm{C}\) water. When water acquires a temperature of \(80^{\circ}\mathrm{C}\), the mass of water present will be: (Take specific heat of water =1 cal g^-1 \(^\circ\)C^-1 and latent heat of steam = 540 cal g^-1)

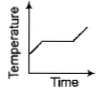
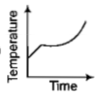
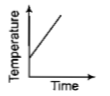
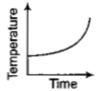
Liquid oxygen at 50K is heated to 300K at constant pressure of 1 atm. The rate of heating is constant.Which one of the following graphs represents the variation of temperature with time?

1. 

2. 

3. 

4. 

The coefficient of linear expansion of brass and steel are ${\alpha }_1$ and ${\alpha }_2$. If we take a brass rod of length $l_1$ and steel rod of length $l_2$ at 0°C, their difference in length $\left(l_2-l_1\right)$ will remain the same at a temperature if

1. ${\alpha }_1{l}_2={\alpha }_2{l}_1$                                 

2. ${\alpha }_1{l}_2^2={\alpha }_2{l}_1^2$

3. ${\alpha }_1^2{l}_1={\alpha }_2^2{l}_2$                                   

4. ${\alpha }_1{l}_1={\alpha }_2{l}_2$