One solid sphere A and another hollow sphere B are of same mass and same outer radii. Their moment of inertia about their diameters are respectively I_A and I_B such that

1. ${\mathrm{I}}_{\mathrm{A}}={\mathrm{I}}_{\mathrm{B}}$

2. ${\mathrm{I}}_{\mathrm{A}}>{\mathrm{I}}_{\mathrm{B}}$

3. ${\mathrm{I}}_{\mathrm{A}}<{\mathrm{I}}_{\mathrm{B}}$

4. $\frac{{\mathrm{I}}_{\mathrm{A}}}{{\mathrm{I}}_{\mathrm{B}}}=\frac{d_A}{d_B}$

A couple produces:   

A wheel of radius R rolls on the ground with a uniform velocity v. The velocity of topmost point relative to the bottommost point is

1. v

2. 2v

3. v/2

4. zero

A constant torque of 1000 N-m turns a wheel of moment of inertial 200 $\mathrm{kg}-{\mathrm{m}}^2$ about an axis through its centre. Its angular velocity after 3 s is

1. 1 rad/s

2. 5 rad/s

3. 10 rad/s

4. 15 rad/s

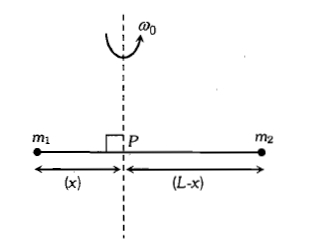
Point masses ${\mathrm{m}}_1$ and ${\mathrm{m}}_2$ are placed at the opposite ends of a rigid of length L and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ${\mathrm{\omega }}_0$ is minimum is given by

$1. \mathrm{x} =\frac{{\mathrm{m}}_1}{{\mathrm{m}}_2}\mathrm{L}$
$2. \mathrm{x} = \frac{{\mathrm{m}}_2}{{\mathrm{m}}_1}\mathrm{L}$
$3. \mathrm{x} = \frac{{\mathrm{m}}_2\mathrm{L}}{{\mathrm{m}}_1+ {\mathrm{m}}_2}$
$4. \mathrm{x} = \frac{{\mathrm{m}}_1\mathrm{L}}{{\mathrm{m}}_1+ {\mathrm{m}}_2}$

$A solid sphere rolls down on an inclined plane of inclination \theta .$
$What is the acceleration as the sphere reaches bottom?$
$\mathbf{[}\mathit{O}\mathit{d}\mathit{i}\mathit{s}\mathit{h}\mathit{a}\mathbf{ }\mathit{J}\mathit{E}\mathit{E}\mathbf{ }\mathbf{2002}\mathbf{,}\mathbf{ }\mathbf{03}\mathbf{;}\mathbf{ }\mathit{C}\mathit{B}\mathit{S}\mathit{E}\mathbf{ }\mathit{P}\mathit{M}\mathit{T}\mathbf{ }\mathbf{2014}\mathbf{]}$
$\left(a\right) \frac{5}{7}gSin\theta \left(b\right) \frac{3}{5}gSin\theta$
$\left(c\right) \frac{2}{7}gSin\theta \left(d\right) \frac{2}{5}gSin\theta$

A wheel is at rest. Its angular velocity increases uniformly and becomes \(80\) rad/s after \(5\) s. The total angular displacement is

Two discs are rotating about their axes, normal to the discs and passing through the centres of the discs. Disc D${}_1$ has a 2 kg mass, 0.2 m radius, and an initial angular velocity of 50 rad s${}^{-1}$. Disc D${}_2$ has 4 kg mass, 0.1 m radius, and initial angular velocity of 200 rad s${}^{-1}$. The two discs are brought in contact face to face, with their axes of rotation coincident. The final angular velocity (in rad.s${}^{-1}$) of the system will be:

1. 60

2. 100

3. 120

4. 40

A body rolls down an inclined plane without slipping. The fraction of total energy associated with its rotation will be

$1. {\mathrm{K}}^2+ {\mathrm{R}}^2$
$2. \frac{{\mathrm{K}}^2}{{\mathrm{R}}^2}$
$3. \frac{{\mathrm{K}}^2}{{\mathrm{K}}^2+ {\mathrm{R}}^2}$
$4. \frac{{\mathrm{R}}^2}{{\mathrm{K}}^2+ {\mathrm{R}}^2}$

Where k is radius of gyration of the body about an axis passing through centre of mass and R is the radius of the body. 

A solid cylinder rolls down an inclined plane that has friction sufficient to prevent sliding. The ratio of rotational energy to total kinetic energy is

1.  $\frac{1}{2}$

2.  $\frac{1}{3}$

3.  $\frac{2}{3}$

4.  $\frac{3}{4}$