A spring 40 mm long is stretched by the application of force. If 10 N force is required to stretch the spring through 1 mm, then work done to stretch the spring 40 mm is equal to:

1.	84 J	2.	68 J
3.	23 J	4.	8 J

Two springs with spring constants $k_1$ = 1500 N/m and $k_2$ = 3000 N/m are stretched by the same force. The ratio of potential energy stored in the springs will be 

1. 2:1

2. 1:2

3. 4:1

4. 1:4

A block of mass \(2~\text{kg}\) moving with a velocity of \(10~\text{m/s}\) on a smooth surface hits a spring of force constant \(80\times10^3~\text{N/m}\) as shown in the figure. The maximum compression in the spring will be:
               
1. \(5~\text{cm}\) 
2. \(10~\text{cm}\)
3. \(15~\text{cm}\)
4. \(20~\text{cm}\)

A particle of mass 10 kg is moving with velocity of $10\sqrt{x}$ m/s, where x is displacement . The work done by net force during the displacement of particle form x = 4 to x = 9 m is 

1. 1250 J

2. 1000 J

3. 3500 J

4. 2500 J

The relation between velocity (v) and time (t) is $\mathrm{v\alpha }\sqrt{\mathrm{t}}$, then which one of the following quantity is constant:

1.  Force

2.  Power

3.  Momentum

4.  Kinetic Energy

A particle is moving on the circular path of the radius (R) with centripetal acceleration $a_c=k^{2}R{t}^2$. Then the correct relation showing power (P) delivered by net force versus time (t) is 

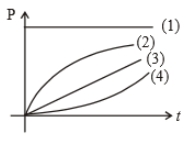
1. 1

2. 2

3. 3

4. 4

A force F is applied on a body which moves with a velocity v in the direction of the force, then the power will be

1.  ${\mathrm{Fv}}^2$

2.  Fv

3.  $\mathrm{F}/{\mathrm{v}}^2$

4.  F/v

A mass m slips along the wall of a semispherical surface of radius R. The velocity at the bottom of the surface is [ MP PMT 1993]

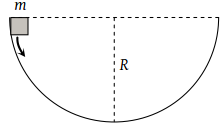
(1) $\sqrt{Rg}$

(2) $\sqrt{2Rg}$

(3) $2\sqrt{\pi Rg}$

(4) $\sqrt{\pi Rg}$

Three different objects of masses $m_1, m_2$ and m₃ are allowed to fall from rest and from the same point ‘O’ along three different frictionless paths. The speeds of the three objects, on reaching the ground, will be in the ratio of 

(1) $m_1:m_2:m_3$

(2) $m_1:2m_2:3m_3$

(3) 1 : 1 : 1

(4) $\frac{1}{m_1}:\frac{1}{m_2}:\frac{1}{m_3}$