A proton (mass m) accelerated by a potential difference V flies through a uniform transverse magnetic field (B). The field occupies a region of space of width 'd'. If 'a' be the angle of deviation of proton from initial direction of motion (Fig), the value of sin $\mathrm{\alpha }$ will be:

1. $\frac{\mathrm{B}}{2}\sqrt{\frac{qd}{mV}}$

2. $\frac{\mathrm{B}}{\mathrm{d}}\sqrt{\frac{q}{2mV}}$

3. $\mathrm{Bd}\sqrt{\frac{\mathrm{q}}{2\mathrm{mV}}}$

4. $\mathrm{qV}\sqrt{\frac{\mathrm{Bd}}{2\mathrm{m}}}$

 

A rectangular loop of sides 10 cm and 5 cm carrying a current I of 12 A, is placed in different orientation as shown in figure below.

(A) 

(B)  

(C) 

(D) 

If there is a uniform magnetic field of 0.3 T in the positive Z-direction in which orientations the loop will be (i) stable equilbrium and (ii) unstable equilibrium:

1. A and D respectively

2. B and D respectively

3. B and C respectively

4. A and B respectively

A positive charge 'q' of mass 'm' is, moving along the +x axis. We wish to apply a uniform magnetic field B for time $∆$t so that the charge reverses its direction crossing the y-axis at a distance 'd'. Then

1. $\mathrm{B} = \frac{2\mathrm{mv}}{\mathrm{qd}} \mathrm{and} ∆\mathrm{t} = \frac{\mathrm{\pi d}}{2\mathrm{v}}$

2. $\mathrm{B} = \frac{\mathrm{mv}}{\mathrm{qd}} \mathrm{and} ∆\mathrm{t} = \frac{\mathrm{\pi d}}{\mathrm{v}}$

3. $\mathrm{B} = \frac{2\mathrm{mv}}{\mathrm{qd}} \mathrm{and} ∆\mathrm{t} = \frac{\mathrm{\pi d}}{\mathrm{v}}$

4. $\mathrm{B} = \frac{\mathrm{mv}}{2\mathrm{qd}} \mathrm{and} ∆\mathrm{t} = \frac{\mathrm{\pi d}}{2\mathrm{v}}$

Consider the three closed loops drawn using solid line in the magnetic field (magnetic field lines are drawn using dotted line) of an infinite curent-carrying wire normal to the plane of paper as shown.

Rank the line integral of the magnetic field along each path in order of increasing magnitude :

(1) 1> 2>3

(2) 1= 3>2

(3) 1=2=3

(4) 3> 2>1

The magnetic flux density B at a distance r from a long straight rod carrying a steady current varies with r as shown in figure.

A long straight, solid metal wire of radius 2 mm carries a current uniformly distributed over its circular cross-section. The magnetic field induction at a distance 2 mm from its axis is B. Then, the magnetic field induction at distance 1 mm from axis will be

(1) B

(2) B/2

(3) 2B

(4) B

Figure shows a cross-section of a large metal sheet carrying an electric current along its surface. The current in a strip of width dl is (Kdl) where K is a constant. Find the magnetic field at a point P at a distance x from the metal strips

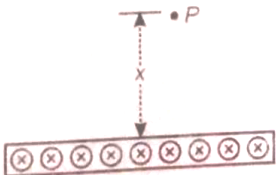
1.  $\frac{1}{2}{\mu }_{0}Kx$

2.  ${\mu }_{0}K$

3.  $\frac{1}{2}{\mu }_{0}K$

4.  $\frac{{\mu }_{0}Kx}{4}$

Three infinitely-long conductors carrying currents $I_1, I_2 and I_3$ lie perpendicular to the plane of the paper as shown below.

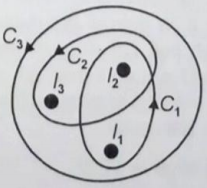
If the value of integral $\oint \overrightarrow{\mathrm{B}}.\overrightarrow{\mathrm{dl}}$ for the loops ${\mathrm{C}}_1, {\mathrm{C}}_2 \mathrm{and} {\mathrm{C}}_3 \mathrm{are} 2{\mathrm{\mu }}_0, 4{\mathrm{\mu }}_0 \mathrm{and} {\mathrm{\mu }}_0$ in the units of N/A, respectively, then

1.  $I_1$ = 3 A into the paper

2.  $l_2$ = 3 A out of the paper

3.  $I_3$ = 0

4.  $I_3$ = 1 A out of the paper

A cylindrical wire of radius R is carrying current i uniformly distributed over its cross-section.  If a circular loop of radius r is taken as amperian loop, then the variation value of $\oint \overrightarrow{B}.\overrightarrow{dl}$ over this loop with radius 'r' of loop will be best represented by:

(1)

(2) 

(3)

(4)