Two monochromatic waves each of amplitude A have a phase difference $\frac{\mathrm{\pi }}{2}$ between them. When they superimpose, the amplitude of the resultant wave is

1.  2A

2.  Zero

3.  4A

4.  $A\sqrt{2}$

A screen is placed 100 cm from a single slit which is illuminated with 5000 $\stackrel{\mathrm{o}}{\mathrm{A}}$ light. If the distance between the first and third minima in the diffraction pattern is 5 mm. The width of the slit is

1.  2 mm

2.  0.2 $\mu$m

3.  $2 \times {10}^{-4} \mathrm{m}$

4.  $4 \times {10}^{-5} \mathrm{m}$

When the light of a certain wavelength is incident on a plane surface of a material of a glancing angle $30°$, the reflected light is polarised. The angle of refraction is

1.  $60°$

2.  $30°$

3.  $45°$

4.  $40°$

In a double-slit experiment, the distance between the slit is d. The screen is at a distance D from the slits and $\lambda$ is the wavelength of light used. If a dark fringe is formed opposite to a slit on the screen, the order of fringe is

1.  $\frac{{\mathrm{d}}^2+\mathrm{\lambda D}}{2\mathrm{\lambda D}}$

2.  $-\frac{\left(\mathrm{D}+\mathrm{d}\right)}{2\mathrm{\lambda }}$

3.  $\frac{\mathrm{D\lambda }+\mathrm{d}}{2\mathrm{D}}$

4.  $\frac{{\mathrm{D}}^2+\mathrm{d\lambda }}{2\mathrm{\lambda }}$

In Y.D.S.E., if a liquid is filled between the space of the screen and slit, then

1.  Central bright fringe will shift upward.

2.  Central bright fringe will not shift.

3.  Central bright fringe will shift downward.

4.  Central fringe may shift downward or upward.

In Y.D.S.E. if the width of the slits is gradually decreased, then

1.  Bright fringe will become brighter and dark fringe becomes darker.

2.  Bright fringe becomes less bright and dark fringe becomes less dark.

3.  Bright fringe becomes brighter and dark fringe becomes lighter.

4.  Bright fringe becomes less bright and dark fringe becomes darker.

In YDSE, two thin transparent films of mica and glass are put in the path of two waves from coherent sources $S_1 \mathrm{and} S_2$. If their thicknesses are 3t and 2t respectively, what should be the refractive index of mica so that central maxima is found at $O\left({\mu }_{glass} = 1.5\right)$?

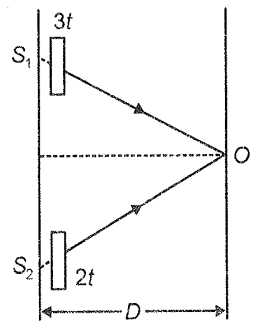
1.  1.25

2.  1.5

3.  1.75

4.  1.33

In Young's double-slit experiment sources of equal intensities are used. The distance between the slits is \(d\) and the wavelength of light used is \(\lambda (\lambda<<d)\). The angular separation of nearest points on either side of central maximum where intensities become half of the maximum value is:
1. \(\frac{\lambda}{d}\)
2. \(\frac{\lambda}{2d}\)
3. \(\frac{\lambda}{4d}\)
4. \(\frac{\lambda}{6d}\)

The angular width of the principal maximum in Fraunhofer single slit diffraction is 0.1 radian. The angular width of second-order secondary maxima is

1.  0.05 radian

2.  0.1 radian

3.  0.5 radian

4.  0.25 radian