Light waves of intensities \(I\) and \(9I\) interfere to produce a fringe pattern on a screen. The phase difference between the waves at point \(P\) is \(\dfrac{3\pi}{2}\) and \(2\pi\) at other point \(Q\). The ratio of intensities at \(P\) and \(Q\) is:
1. \(8:5\)
2. \(5:8\)
3. \(1:4\)
4. \(9:1\)

In YDSE, two thin transparent films of mica and glass are put in the path of two waves from coherent sources $S_1 \mathrm{and} S_2$. If their thicknesses are 3t and 2t respectively, what should be the refractive index of mica so that central maxima is found at $O\left({\mu }_{glass} = 1.5\right)$?

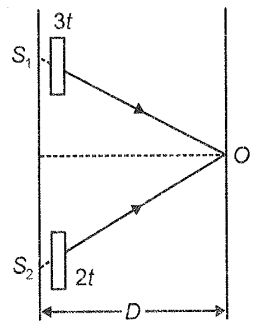
1.  1.25

2.  1.5

3.  1.75

4.  1.33

In Young's double-slit experiment sources of equal intensities are used. The distance between the slits is \(d\) and the wavelength of light used is \(\lambda (\lambda<<d)\). The angular separation of nearest points on either side of central maximum where intensities become half of the maximum value is:
1. \(\frac{\lambda}{d}\)
2. \(\frac{\lambda}{2d}\)
3. \(\frac{\lambda}{4d}\)
4. \(\frac{\lambda}{6d}\)

The angular width of the principal maximum in Fraunhofer single slit diffraction is 0.1 radian. The angular width of second-order secondary maxima is

1.  0.05 radian

2.  0.1 radian

3.  0.5 radian

4.  0.25 radian

The slits in a double-slit interference experiment are illuminated by a light of wavelength $\lambda$ = 600 nm. A thin transparent sheet of thickness t is placed in front of one of the slits. The number of fringes shifting is plotted across the refractive index $\mu$ of the sheet as given. The value of t is

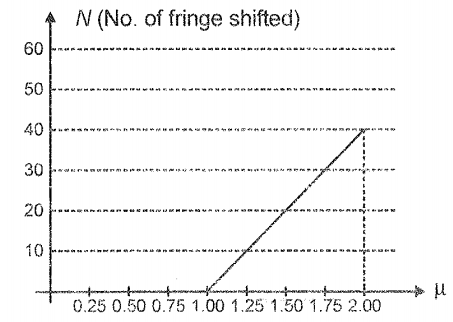
1.  2.4 $\mu$m

2.  24 $\mu$m

3.  4.8 $\mu$m

4.  48 $\mu$m

In Young's double-slit experiment, the distance between the slits is 1 mm. The wavelength of the light used is 600 nm. Fringe width of the interference pattern (as shown in the figure) is :

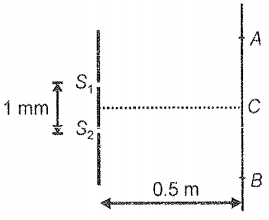
1.  0.6 mm

2.  0.3 mm

3.  0.4 mm

4.  0.2 mm

Four coherent sources of intensity \(I\) are superimposed constructively at a point. The intensity at that point is:
1. \(4I\)
2. \(8I\)
3. \(16I\)
4. \(24I\)

In Young's double-slit experiment, the intensities at the points of maxima and minima are $l_0$ and zero respectively. Intensities of individual sources are

1.  $4l_0$

2.  $\frac{l_0}{2}$

3. $2l_0$

4.  $\frac{l_0}{4}$

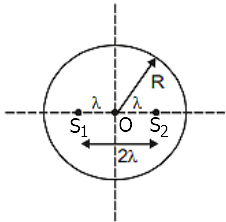
Two coherent light sources $S_1 \mathrm{and} S_2$ are kept at equal distances $\lambda$from the center of the circle on the same plane of the circle as shown in the figure. In one complete revolution on the circular path, the number of maxima observed is: ($\mathrm{\lambda }$= wavelength of light used and 2λ<<R)

1.  4

2.  6

3.  8

4.  12

The ratio of intensities in consecutive maximas in a diffraction pattern due to a single slit is

1.  $1 : \frac{4}{9{\pi }^2} : \frac{4}{25{\pi }^2}$

2.  $1 : \frac{4}{9} : \frac{4}{25}$

3.  $1 : \frac{4}{{\pi }^2} : \frac{9}{{\pi }^2}$

4.  1: 4: 9