In the three figures, each wire has a mass M, radius R and a uniform mass distribution. If they form part of a circle of radius R, then about an axis perpendicular to the plane and passing through the centre (shown by crosses), their moment of inertia is in the order:
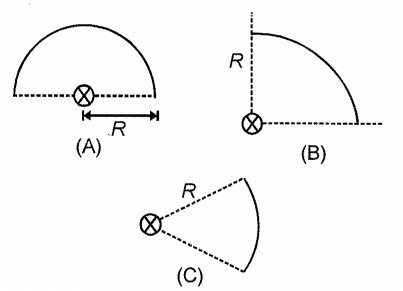
1.
2.
3.
4.

The law of conservation of angular momentum is valid when:
| 1. | The net force is zero and the net torque is non-zero | 2. | The net force is non-zero and the net torque is non zero |
| 3. | Net force may or may not be zero and net torque is zero | 4. | Both force and torque must be zero |
| 1. | \(\vec{\tau}=(-17 \hat{\mathrm{i}}+6 \hat{\mathrm{j}}+4 \widehat{\mathrm{k}})\) N-m |
| 2. | \(\vec{\tau}=(-17 \hat{\mathrm{i}}+6 \hat{\mathrm{j}}-4 \widehat{\mathrm{k}}) \) N-m |
| 3. | \(\vec{\tau}=(17 \hat{\mathrm{i}}-6 \hat{\mathrm{j}}+4 \widehat{\mathrm{k}})\) N-m |
| 4. | \(\vec{\tau}=(-41 \hat{\mathrm{i}}+6 \hat{\mathrm{j}}+16 \hat{\mathrm{k}})\) N-m |

1. \(\frac{5}{3}mL^2\)
2. \(4mL^2\)
3. \(\frac{1}{4}mL^2\)
4. \(\frac{2}{3}mL^2\)
The mass per unit length of a non-uniform rod of length \(L\) is given by \(\mu =λx^{2}\) where \(\lambda\) is a constant and \(x\) is the distance from one end of the rod. The distance between the centre of mass of the rod and this end is:
| 1. | \(\frac{L}{2}\) | 2. | \(\frac{L}{4}\) |
| 3. | \(\frac{3L}{4}\) | 4. | \(\frac{L}{3}\) |
A particle of mass \(M\) revolves in a circular path of radius \(R\) with constant angular momentum \(L\). The linear momentum of the particle is:
| 1. | \(\dfrac{L}{MR}\) | 2. | \(\dfrac{L}{R}\) |
| 3. | \(\dfrac{L^2}{MR^2}\) | 4. | \(\dfrac{MR}{L}\) |
Four masses are joined to light circular frames as shown in the figure. The radius of gyration of this system about an axis passing through the center of the circular frame and perpendicular to its plane would be:
(where '\(a\)' is the radius of the circle)

1. \(\frac{a}{\sqrt{2}}\)
2. \(\frac{a}{{2}}\)
3. \(a\)
4. \(2a\)
A solid sphere of mass \(M\) and the radius \(R\) is in pure rolling with angular speed \(\omega\) on a horizontal plane as shown in the figure. The magnitude of the angular momentum of the sphere about the origin \(O\) is:

1. \(\frac{7}{5} M R^{2} \omega\)
2. \(\frac{3}{2} M R^{2} \omega\)
3. \(\frac{1}{2} M R^{2} \omega\)
4. \(\frac{2}{3} M R^{2} \omega\)
A uniform square plate \(ABCD\) has a mass of \(10\) kg.
If two point masses of \(5\) kg each are placed at the corners \(C\) and \(D\) as shown in the adjoining figure, then the centre of mass shifts to the mid-point of:

1. \(OH\)
2. \(DH\)
3. \(OG\)
4. \(OF\)
Two particles of mass \(5~\text{kg}\) and \(10~\text{kg}\) respectively are attached to the two ends of a rigid rod of length \(1~\text{m}\) with negligible mass. The centre of mass of the system from the \(5~\text{kg}\) particle is nearly at a distance of:
1. \(50~\text{cm}\)
2. \(67~\text{cm}\)
3. \(80~\text{cm}\)
4. \(33~\text{cm}\)






