The velocity of water in a river is:

1.	same everywhere.
2.	more in the middle and less near its banks.
3.	less in the middle and more at banks.
4.	increases from one bank to other.

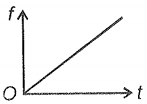
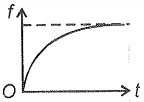
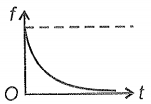
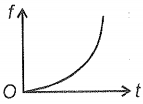
A steel ball is dropped on the water surface from zero height. The variation of the viscous force with time on the ball can be represented as

1.  

2.  

3.  

4.  

A body with an air cavity loses one-third of weight when immersed in water. If the relative density of the material of the body is 6, then the ratio of the volume of the cavity to the volume of the body is:

1.  $\frac{1}{2}$

2.  $\frac{2}{3}$

3.  $\frac{3}{4}$

4.  $\frac{4}{5}$

Which of the following graphs correctly shows the variation in kinetic energy (KE) of a metal sphere falling freely in a lake? Assume sufficient depth of the lake to impart terminal velocity to the sphere (d: depth)

1.              2. 
3.             4. 

If an incompressible liquid is flowing through a horizontal pipe having branches of area \(\mathrm{A},\) \(0.4\mathrm{A},\) and \(0.5\mathrm{A}\) as shown in the figure, then the value of \(\mathrm{v}\) is:
                               
1. 3.2 m/s
2. 6.4 m/s
3. 1.6 m/s
4. 0.8 m/s

The continuity equation for fluid flow is based on the principle of the

(1) Conservation of mass

(2) Conservation of energy

(3) Conservation of momentum

(4) Conservation of angular momentum

Blood flows in an artery of radius R in a Laminar manner under pressure p with a flow rate Q. If the radius gets halved and the pressure quadruples, the new rate of flow will be

1.  4Q

2.  $\frac{\mathrm{Q}}{4}$

3.  Q

4.  $\frac{Q}{8}$

A sphere of mass M and radius R is falling in a viscous liquid. The terminal velocity attained by the sphere will be proportional to:

(1) ${\mathrm{R}}^2$

(2) R

(3) $\frac{1}{\mathrm{R}}$

(4) $\frac{1}{{\mathrm{R}}^2}$

Two water droplets merge with each other to form a larger droplet isothermally. In this process

(1) Energy is absorbed

(2) Energy is liberated

(3) Energy is neither liberated nor absorbed

(4) Some mass is converted into energy

From the given diagram, what is the velocity \(v_3?\)
               
1. \(4~\text{m/s}\)
2. \(3~\text{m/s}\)
3. \(1~\text{m/s}\)
4. \(2~\text{m/s}\)