When a projectile of mass 2 kg is projected from the top of a tower of height 20 m with velocity 10 m/s in the horizontal direction, then angular momentum about the lowermost point of the tower when it touches the ground is:

(1) 600 kg ${\mathrm{m}}^2/\mathrm{s}$

(2) 400 kg ${\mathrm{m}}^2/\mathrm{s}$

(3) 800 kg ${\mathrm{m}}^2/\mathrm{s}$

(4) Zero

The rotational analouge of equation \(F=\frac{mdv}{dt}\) is:

A disc of mass \(M\) and radius \(R\) starts falling down as shown in the figure. The string unwinds without slipping on the disc. The instantaneous power developed by the tension is:

     
1. \((T\times R \omega)\)
2. \((T\times R \omega)/2\)
3. \(2(T\times R \omega)\)
4. zero

Four masses are joined to light circular frames as shown in the figure. The radius of gyration of this system about an axis passing through the center of the circular frame and perpendicular to its plane would be:
(where '\(a\)' is the radius of the circle)
                        
1. \(\frac{a}{\sqrt{2}}\)
2. \(\frac{a}{{2}}\)
3. \(a\)
4. \(2a\)

Two particles of mass \(5~\text{kg}\) and \(10~\text{kg}\) respectively are attached to the two ends of a rigid rod of length \(1~\text{m}\) with negligible mass. The centre of mass of the system from the \(5~\text{kg}\) particle is nearly at a distance of:
1. \(50~\text{cm}\)
2. \(67~\text{cm}\)
3. \(80~\text{cm}\)
4. \(33~\text{cm}\)

What would be the torque about the origin when a force \(3\hat{j}~\text N\) acts on a particle whose position vector is \(2\hat{k}~\text m?\)

The masses ${\mathrm{m}}_1 \mathrm{and} {\mathrm{m}}_2 \left(\mathrm{with} {\mathrm{m}}_1 < {\mathrm{m}}_2\right)$ are connected to the two ends of a compressed spring. Now, when the masses are released on a smooth surface, they will move away with

(1)  the same magnitude of the force.

(2)  the equal magnitude of linear momentum.

(3)  the greater kinetic energy of the first body than that of the second body.

(4)  All of these

Internal forces cannot change:

(1)  the kinetic energy of a system.

(2)  the mechanical energy of a system.

(3)  the momentum of a system.

(4)  all of these

The angular speed of the wheel of a vehicle is increased from 360 rpm to 1200 rpm in 14 seconds. Its angular acceleration is

\(1.~2\pi ~rad/s^{2}\)
\(2.~28\pi ~rad/s^{2}\)
\(3.~120\pi ~rad/s^{2}\)
\(4.~\pi ~rad/s^{2}\)

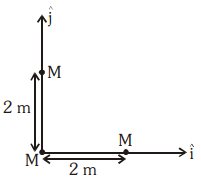
Three identical spheres, each of mass M, are placed at the corners of a right-angle triangle with mutually perpendicular sides equal to 2 m (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of the center of mass.

1. $2(\hat{\mathrm{i}}+\hat{\mathrm{j}})$

2. $(\hat{\mathrm{i}}+\hat{\mathrm{j}})$

3. $\frac{2}{3}(\hat{\mathrm{i}}+\hat{\mathrm{j}})$

4. $\frac{4}{3}(\hat{\mathrm{i}}+\hat{\mathrm{j}})$