If $\overrightarrow{\mathrm{A}} + \overrightarrow{\mathrm{B}}$ is perpendicular to $\overrightarrow{\mathrm{A}} - \overrightarrow{\mathrm{B}}$  , then which of the following statement is correct?

1. $\left|\overrightarrow{\mathrm{A}}\right| = \left|\overrightarrow{\mathrm{B}}\right|$

2. $\overrightarrow{\mathrm{A}} \perp \overrightarrow{\mathrm{B}}$

3. $\overrightarrow{\mathrm{A}}·\overrightarrow{\mathrm{B}} = \mathrm{zero}$

4. $\left(\overrightarrow{\mathrm{A}} + \overrightarrow{\mathrm{B}}\right)·\left(\overrightarrow{\mathrm{A}} - \overrightarrow{\mathrm{B}}\right) \ne 0$

The angle between the two vectors \(\left(- 2 \hat{i} +3 \hat{j} + \hat{k}\right)\) and \(\left(\hat{i} + 2 \hat{j} - 4 \hat{k}\right)\) is:
1. \(0^{\circ}\)
2. \(90^{\circ}\)
3. \(180^{\circ}\)
4. \(45^{\circ}\)

If $\overrightarrow{\mathrm{a}} + \overrightarrow{\mathrm{b}} + \overrightarrow{\mathrm{c}} = \overrightarrow{0}$; then which of the following statements is incorrect?

(1) $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}} \mathrm{and} \overrightarrow{\mathrm{c}}$ must each be a null vector.

(2) The magnitude of $\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}$ equals the magnitude of $\overrightarrow{\mathrm{c}}$.

(3) The magnitude of ä can never be greater than the sum of the magnitudes of $\overrightarrow{\mathrm{b}}$ and $\overrightarrow{\mathrm{c}}$

(4) ä must lie in the plane of $\overrightarrow{\mathrm{b}}$ and $\overrightarrow{\mathrm{c}}$.

When a force of magnitude F acts on a body of mass m the acceleration produced in the body is a. If three coplanar forces of equal magnitude F act on the same body as shown in the figure, then acceleration produced is

1.  0

2.  $\left(\sqrt{3} +\hspace{0.17em}1\right)\mathrm{a}$

3.  $\left(\sqrt{3} -\hspace{0.17em}1\right)\mathrm{a}$

4.  $\sqrt{3}\mathrm{a}$

Three forces each of magnitude 1 N act along with the sides AB, BC, and CD of a regular hexagon. The magnitude of their resultant is:

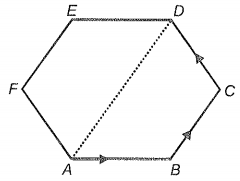
(1) 4N 

(2) Zero

(3) 2 N

(4) 1 N

If a unit vector \(\hat j\) is rotated through an angle of \(45^{\circ}\) anticlockwise, then the new vector will be:
1. \(\sqrt{2}\hat i + \sqrt{2}\hat j\)
2. \(\hat i + \hat j\)
3. \(\frac{1}{\sqrt{2}}\hat i + \frac{1}{\sqrt{2}}\hat j\)
4. \(-\frac{1}{\sqrt{2}}\hat i + \frac{1}{\sqrt{2}}\hat j\)

If $\overrightarrow{\mathrm{a}} = 2\hat{\mathrm{i}} + \hat{\mathrm{j}}$ and $\overrightarrow{\mathrm{b}} = 3\hat{\mathrm{i}} + 2\hat{\mathrm{j}}$, then $\left|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}\right|=?$ 

$\stackrel{}{\mathrm{}}$\(\overrightarrow A\) and \(\overrightarrow {B}\) are two vectors given by \(\overrightarrow {A}= 2\hat i + 3\hat j\) and \(\overrightarrow {B}= \hat i + \hat j\). The component of \(\overrightarrow A\) parallel to \(\overrightarrow B\) is:
1. \(\frac{(2\hat i -\hat j)}{2}\)
2. \(\frac{5}{2}(\hat i - \hat j)\)
3. \(\frac{5}{2}(\hat i + \hat j)\)
4. \(\frac{(3\hat i -2\hat j)}{2}\)

If a vector is inclined at angles \(\alpha ,\beta ,~\text{and}~\gamma\), with \(x\), \(y\), and \(z\)-axis respectively, then the value of \(\sin^{2}\alpha+\sin^{2}\beta+ \sin^{2}\gamma\)${}^{}$
is equal to:
1. \(0\)
2. \(1\)
3. \(2\)
4. \(\frac{1}{2}\)

If $\hat{\mathrm{p}}$ is the unit vector in the direction $\overrightarrow{\mathrm{B}}$, then:

1.  $\hat{\mathrm{p}} = \frac{\left|\overrightarrow{\mathrm{B}}\right|}{\overrightarrow{\mathrm{B}}}$

2.  $\hat{\mathrm{p}} = \left|\overrightarrow{\mathrm{B}}\right| \times \overrightarrow{\mathrm{B}}$

3.  $\hat{\mathrm{p}} = \frac{\overrightarrow{\mathrm{B}}}{\left|\overrightarrow{\mathrm{B}}\right|}$

4.  $\hat{\mathrm{p}} = \frac{\overrightarrow{\mathrm{B}}}{\overrightarrow{\mathrm{B}}}$