If a unit vector \(\hat j\) is rotated through an angle of \(45^{\circ}\) anticlockwise, then the new vector will be:
1. \(\sqrt{2}\hat i + \sqrt{2}\hat j\)
2. \(\hat i + \hat j\)
3. \(\frac{1}{\sqrt{2}}\hat i + \frac{1}{\sqrt{2}}\hat j\)
4. \(-\frac{1}{\sqrt{2}}\hat i + \frac{1}{\sqrt{2}}\hat j\)

If $\overrightarrow{\mathrm{a}} = 2\hat{\mathrm{i}} + \hat{\mathrm{j}}$ and $\overrightarrow{\mathrm{b}} = 3\hat{\mathrm{i}} + 2\hat{\mathrm{j}}$, then $\left|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}\right|=?$ 

$\stackrel{}{\mathrm{}}$\(\overrightarrow A\) and \(\overrightarrow {B}\) are two vectors given by \(\overrightarrow {A}= 2\hat i + 3\hat j\) and \(\overrightarrow {B}= \hat i + \hat j\). The component of \(\overrightarrow A\) parallel to \(\overrightarrow B\) is:
1. \(\frac{(2\hat i -\hat j)}{2}\)
2. \(\frac{5}{2}(\hat i - \hat j)\)
3. \(\frac{5}{2}(\hat i + \hat j)\)
4. \(\frac{(3\hat i -2\hat j)}{2}\)

If a vector is inclined at angles \(\alpha ,\beta ,~\text{and}~\gamma\), with \(x\), \(y\), and \(z\)-axis respectively, then the value of \(\sin^{2}\alpha+\sin^{2}\beta+ \sin^{2}\gamma\)${}^{}$
is equal to:
1. \(0\)
2. \(1\)
3. \(2\)
4. \(\frac{1}{2}\)

If $\hat{\mathrm{p}}$ is the unit vector in the direction $\overrightarrow{\mathrm{B}}$, then:

1.  $\hat{\mathrm{p}} = \frac{\left|\overrightarrow{\mathrm{B}}\right|}{\overrightarrow{\mathrm{B}}}$

2.  $\hat{\mathrm{p}} = \left|\overrightarrow{\mathrm{B}}\right| \times \overrightarrow{\mathrm{B}}$

3.  $\hat{\mathrm{p}} = \frac{\overrightarrow{\mathrm{B}}}{\left|\overrightarrow{\mathrm{B}}\right|}$

4.  $\hat{\mathrm{p}} = \frac{\overrightarrow{\mathrm{B}}}{\overrightarrow{\mathrm{B}}}$

Which of the following sets of forces cannot give zero resultant?

(1) 3 N, 4 N, 5 N

(2) 9 N, 8 N, 7 N

(3) 16 N, 2 N, 17 N

(4) 30 N, 5 N, 24 N

If two force vectors $\overrightarrow{\mathrm{A}} \mathrm{and} \overrightarrow{\mathrm{B}}$ of the same magnitude are arranged in the following manner, the magnitude of resultant is maximum for?

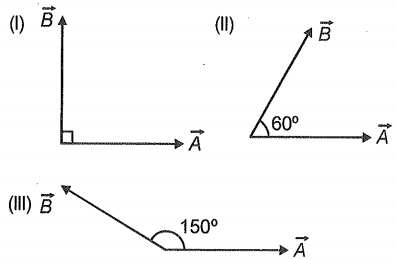
(1) (I)

(2) (II)

(3) Both (II) & (III)

(4) Both (I) & (II)

The minimum number of non-coplanar vectors whose vector sum can be zero is:

(1) 2

(2) 3

(3) 4

(4) 5

The resultant vector of $\overrightarrow{\mathrm{P}} \mathrm{and} \overrightarrow{\mathrm{Q}}$ makes angle ${\mathrm{\theta }}_1$ with $\overrightarrow{\mathrm{P}}$ and ${\mathrm{\theta }}_2$ with $\overrightarrow{\mathrm{Q}}$.Then-

1.  ${\mathrm{\theta }}_1 > {\mathrm{\theta }}_2$

2.  ${\mathrm{\theta }}_1 < {\mathrm{\theta }}_2 \mathrm{if} \mathrm{P} > \mathrm{Q}$

3.  ${\mathrm{\theta }}_1 < {\mathrm{\theta }}_2 \mathrm{if} \mathrm{P} < \mathrm{Q}$

4.  ${\mathrm{\theta }}_1 > {\mathrm{\theta }}_2 \mathrm{if} \mathrm{P} = \mathrm{Q}$

The figure shows ABCDEF as a regular hexagon. What is the value of $\overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{AC}} + \overrightarrow{\mathrm{AD}} + \overrightarrow{\mathrm{AE}} + \overrightarrow{\mathrm{AF}}$?

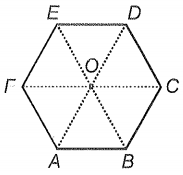
1.  $\overrightarrow{\mathrm{AO}}$

2.  $2\overrightarrow{\mathrm{AO}}$

3.  $4\overrightarrow{\mathrm{AO}}$

4.  $6\overrightarrow{\mathrm{AO}}$