A person sitting on the ground floor of a building notices through the window, of height \(1.5~\text{m}\), a ball dropped from the roof of the building crosses the window in \(0.1~\text{s}\). What is the velocity of the ball when it is at the topmost point of the window? \(\left(g = 10~\text{m/s}^2\right )\)
1.
\(15.5~\text{m/s}\)
2.
\(14.5~\text{m/s}\)
3.
\(4.5~\text{m/s}\)
4.
\(20~\text{m/s}\)
When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity \({v_0}\) and the braking capacity, or deceleration, \(-a\) that is caused by the braking. Expression for stopping distance of a vehicle in terms of \({v_0}\) and \(a\) is:
| 1. | \(\dfrac{{v_o}^2}{2a}\) | 2. | \(\dfrac{{v_o}}{2a}\) |
| 3. | \(\dfrac{{v_o}^2}{a}\) | 4. | \(\dfrac{2a}{{v_o}^2}\) |
A ball is bouncing elastically with a speed of \(1~\text{m/s}\) between the walls of a railway compartment of size \(10~\text m\) in a direction perpendicular to the walls. The train is moving at a constant velocity of \(10~\text{m/s}\) parallel to the direction of motion of the ball. As seen from the ground:
| (a) | the direction of motion of the ball changes every \(10\) sec. |
| (b) | the speed of the ball changes every \(10\) sec. |
| (c) | the average speed of the ball over any \(20\) sec intervals is fixed. |
| (d) | the acceleration of the ball is the same as from the train. |
Choose the correct option:
| 1. | (a), (c), (d) | 2. | (a), (c) |
| 3. | (b), (c), (d) | 4. | (a), (b), (c) |
If in one-dimensional motion, instantaneous speed \(v\) satisfies \(0\leq v<v_0,\) then:
| 1. | the displacement in time \(T\) must always take non-negative values. |
| 2. | the displacement \(x\) in time \(T\) satisfies \(-{v_0T} \lt x \lt {v_0T}.\) |
| 3. | the acceleration is always a non-negative number. |
| 4. | the motion has no turning points. |
The position of an object moving along the \(x\text-\)axis is given by, \(x=a+bt^2\), where \(a=8.5 ~\text m,\) \(b=2.5~\text{m/s}^2,\) and \(t\) is measured in seconds. Its velocity at \(t=2.0~\text s\) will be:
1. \(13~\text{m/s}\)
2. \(17~\text{m/s}\)
3. \(10~\text{m/s}\)
4. \(0~\text{m/s}\)
A small block slides down on a smooth inclined plane starting from rest at time \(t=0.\) Let \(S_n\) be the distance traveled by the block in the interval \(t=n-1\) to \(t=n.\) Then the ratio \(\dfrac{S_n}{S_{n +1}}\) is:
| 1. | \(\dfrac{2n+1}{2n-1}\) | 2. | \(\dfrac{2n}{2n-1}\) |
| 3. | \(\dfrac{2n-1}{2n}\) | 4. | \(\dfrac{2n-1}{2n+1}\) |
A body is thrown upwards and reaches its maximum height. At that position:
| 1. | its velocity is zero and its acceleration is also zero. |
| 2. | its velocity is zero but its acceleration is maximum. |
| 3. | its acceleration is minimum. |
| 4. | its velocity is zero and its acceleration is the acceleration due to gravity. |
Which one of the following displacement-time graph represents two moving objects \(P\) and \(Q\) with zero relative velocity?
| 1. | 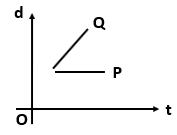 |
2. | 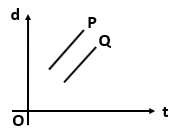 |
| 3. | 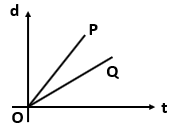 |
4. | 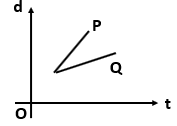 |
A body is projected vertically in the upward direction from the surface of the earth. If the upward direction is taken as positive, then the acceleration of the body during its upward and downward journey is:
| 1. | Positive, negative | 2. | Negative, negative |
| 3. | Positive, positive | 4. | Negative, positive |
When the velocity of a body is variable, then:
| 1. | its speed may be constant |
| 2. | its acceleration may be constant |
| 3. | its average acceleration may be constant |
| 4. | all of the above |






