A particle is moving along the path y = ${\mathrm{x}}^2$ from x = 0 m to x = 2 m. Then the distance traveled by the particle is:

1.  4 m

2.  $\sqrt{20} \mathrm{m}$

3.  $>\sqrt{20} \mathrm{m}$

4.  $<\sqrt{20} \mathrm{m}$

Six particles situated at the corners of a regular hexagon of side \(a\) move at constant speed \(v\). Each particle maintains a direction towards the particle at the next. The time which the particles will take to meet each other is:
1. \(\frac{2 a}{v}~\text{sec}\)
2. \(\frac{a}{v}~\text{sec}\)
3. \(\frac{2 a}{3v}~\text{sec}\)
4. \(\frac{3 a}{v}~\text{sec}\)

A body is projected with velocity $20\sqrt{3}$ m/s with an angle of projection 60$°$ with horizontal. Calculate velocity on that point where body makes an angle 30$°$ with the horizontal.

1. 20 m/s

2. $\frac{20}{\sqrt{3}} m/s$

3. $10\sqrt{3} m/s$

4. 10 m/s

In a uniform circular motion, which of the following quantity is not constant

1. Angular momentum

2. Speed

3. Kinetic energy

4. Momentum

A particle is moving with veocity $\overrightarrow{\mathrm{v}}=\mathrm{k}(\mathrm{y}\hat{\mathrm{i}}+\mathrm{x}\hat{\mathrm{j}})$; where k is constant. The general equation for the path is:

1. $\mathrm{y}={\mathrm{x}}^2+\mathrm{constant}$

2. ${\mathrm{y}}^2={\mathrm{x}}^2+\mathrm{constant}$

3. $\mathrm{y}=\mathrm{x}+\mathrm{constant}$

4. xy=constant

A particle is projected with a velocity u making an angle $\mathrm{\theta }$ with the horizontal. At any instant, its velocity v is at right angles to its initial velocity u; then v is:

1.  ucos$\mathrm{\theta }$

2.  utan$\mathrm{\theta }$

3.  ucot$\mathrm{\theta }$

4.  usec$\mathrm{\theta }$

A projectile is given an initial velocity of $\hat{i}+2\hat{j}$. The cartesian equation of its path is (g = 10 ${\mathrm{ms}}^{-2}$) 

1. $\mathrm{y}=2\mathrm{x}-5{\mathrm{x}}^2$

2. $\mathrm{y}=\mathrm{x}-5{\mathrm{x}}^2$

3. $4\mathrm{y}=2\mathrm{x}-5{\mathrm{x}}^2$

4. $\mathrm{y}=2\mathrm{x}-25{\mathrm{x}}^2$

A ship A is moving westwards with a speed of 10 km ${\mathrm{h}}^{-1}$ and a ship B, 100 km south of A is moving northwards with a speed of 10 km ${\mathrm{h}}^{-1}$. The time after which the distance between them becomes the shortest, is:

1. 5 hr

2. $5\sqrt{2}$ hr

3. $10\sqrt{2}$ hr

4. 0 hr

Time taken by the projectile to reach from A to B is t. Then the distance AB is equal to :

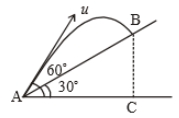
1. $\frac{ut}{\sqrt{3}}$

2. $\frac{\sqrt{3}ut}{2}$

3. $\sqrt{3}ut$

4. 2ut

A particle projected with kinetic energy ${\mathrm{k}}_0$ with an angle of projection $\mathrm{\theta }$. Then the variation of kinetic K with vertical displacement y is

1.  linear

2.  parabolic

3.  hyperbolic

4.  periodic