A steel wire can withstand a load up to 2940 N. A load of 150 kg is suspended from a rigid support. The maximum angle through which the wire can be displaced from the mean position, so that the wire does not break when the load passes through the position of equilibrium, is (2008 E)
1. 30
2. 60
3. 80
4. 85
A sphere of mass m moving with constant velocity hits another sphere of the same mass at rest. If e is the coefficient of restitution. The ratio of their velocities after the collision is
1. 1 + e
2.
3.
4.
A body is thrown vertically up with a certain initial velocity. The potential and the kinetic energy of the body are equal at a point P in its path. If the same body is thrown with double the velocity upwards, the ratio of the potential and the kinetic energies of the body when it crosses at the same point will be:
1. 1:1
2. 1:4
3. 1:7
4. 1:8
A body is displaced from (0,0) to (1m,1m) along the path x=y by a force . The work done by this force will be :
1.
2.
3.
4.
A stone is projected from a horizontal plane. It attains maximum height \(H,\) and strikes a stationary smooth wall & falls on the ground vertically below the maximum height. Assuming the collision to be elastic, the height of the point on the wall where the ball will strike will be:

| 1. | \(\dfrac{H}{2} \) | 2. | \(\dfrac{H}{4} \) |
| 3. | \(\dfrac{3 H}{4} \) | 4. | None of these |
A weightless rod of length 2l carries two equal mass 'm', one tied at lower end A and the other at the middle of the rod at B. The rod can rotate in a vertical plane about a fixed horizontal axis passing through C. The rod is released from rest in the horizontal position. The speed of the mass B at the instant rod becomes vertical is:

1. \(\sqrt{\frac{3 g l}{5}} \)
2. \(\sqrt{\frac{4 g l}{5}} \)
3. \(\sqrt{\frac{6 g l}{5}} \)
4. \(\sqrt{\frac{7 g l}{5}} \)
A force F is applied on a body which moves with a velocity v in the direction of the force, then the power will be
1.
2. Fv
3.
4. F/v
Potential energy \((U)\) related to coordinates is given by; \(U=3(x+y).\) Work done by the conservative force when the particle is going from \((0,0), (2,3)\) is:
1. \(15\) J
2. \(-15\) J
3. \(12\) J
4. \(10\) J
A mass m slips along the wall of a semispherical surface of radius R. The velocity at the bottom of the surface is [ MP PMT 1993]
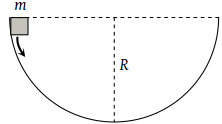
1.
2.
3.
4.
Three different objects of mass and m3 are allowed to fall from rest and from the same point ‘O’ along three different frictionless paths. The speeds of the three objects, on reaching the ground, will be in the ratio of:
| 1. | 2. | ||
| 3. | 1 : 1 : 1 | 4. |






