A particle which is constrained to move along the x-axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as . Here k and a are positive constants. For , the functional form of the potential energy U(x) of the particle is-
(1) 
(2) 
(3) 
(4) 




A force F acting on an object varies with distance x as shown here. The force is in newton and x in metre. The work done by the force in moving the object from x = 0 to x = 6 m is
(1) 4.5 J
(2) 13.5 J
(3) 9.0 J
(4) 18.0 J
The potential energy of a system is represented in the first figure. the force acting on the system will be represented by:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
A particle, initially at rest on a frictionless horizontal surface, is acted upon by a horizontal force which is constant in size and direction. A graph is plotted between the work done (W) on the particle, against the speed of the particle, (v). If there are no other horizontal forces acting on the particle the graph would look like
1.
2.
3.
4.
Which of the following graphs is correct between kinetic energy (E), potential energy (U) and height (h) from the ground of the particle
1.
2.
3.
4.
The force acting on a body moving along x-axis varies with the position of the particle as shown in the fig.
The body is in stable equilibrium at
1. x = x1
2. x = x2
3. both x1 and x2
4. neither x1 nor x2
The potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
1. C
2. B
3. B and C
4. A and D
Figure shows the F-x graph. Where F is the force applied and x is the distance covered by the body along a straight line path. Given that F is in newton and x in metre, what is the work done ?
1. 10 J
2. 20 J
3. 30 J
4. 40 J
The force required to stretch a spring varies with the distance as shown in the figure. If the experiment is performed with the above spring of half length, the line OA will
1. Shift towards F-axis
2. Shift towards X-axis
3. Remain as it is
4. Become double in length
The graph between \(E\) and \(v\) is:
| 1. |  |
2. |  |
| 3. | 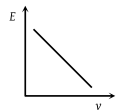 |
4. |  |




















