A parallel plate condenser has a uniform electric field \(E\)(V/m) in the space between the plates. If the distance between the plates is \(d\)(m) and area of each plate is \(A(\text{m}^2)\), the energy (joule) stored in the condenser is:
1.
\(\dfrac{1}{2}\varepsilon_0 E^2\)
2.
\(\varepsilon_0 EAd\)
3.
\(\dfrac{1}{2}\varepsilon_0 E^2Ad\)
4.
\(\dfrac{E^2Ad}{\varepsilon_0}\)
A parallel-plate capacitor of area A, plate separation d, and capacitance C is filled with four dielectric materials having dielectric constants and as shown in the figure below. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by
1.
2.
3.
4.
The diagrams below show regions of equipotentials.
| 1. | the maximum work is required to move \(q\) in figure(iii). |
| 2. | in all four cases, the work done is the same. |
| 3. | the minimum work is required to move \(q\) in the figure(i). |
| 4. | the maximum work is required to move \(q\) in figure(ii). |
A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of the resulting system:
| 1. | decreases by a factor of \(2\) |
| 2. | remains the same |
| 3. | increases by a factor of \(2\) |
| 4. | increases by a factor of \(4\) |
The electrostatic force between the metal plates of an isolated parallel plate capacitor \(C\) having a charge \(Q\) and area \(A\) is:
| 1. | independent of the distance between the plates. |
| 2. | linearly proportional to the distance between the plates. |
| 3. | proportional to the square root of the distance between the plates. |
| 4. | inversely proportional to the distance between the plates. |
A capacitor of \(2~\mu\text{F}\) is charged as shown in the figure. When the switch \({S}\) is turned to position \(2,\) the percentage of its stored energy dissipated is:
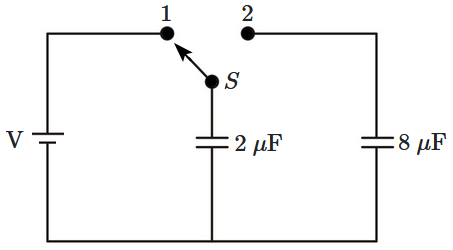
2. \(75\%\)
3. \(80\%\)
4. \(0\%\)
If potential \([\text{in volts}]\) in a region is expressed as \(V[x,y,z] = 6xy-y+2yz,\) the electric field \([\text{in N/C}]\) at point \((1, 1, 0)\) is:
| 1. | \(- \left(3 \hat{i} + 5 \hat{j} + 3 \hat{k}\right)\) | 2. | \(- \left(6 \hat{i} + 5 \hat{j} + 2 \hat{k}\right)\) |
| 3. | \(- \left(2 \hat{i} + 3 \hat{j} + \hat{k}\right)\) | 4. | \(- \left(6 \hat{i} + 9 \hat{j} + \hat{k}\right)\) |
A parallel plate air capacitor has capacitance \(C,\) the distance of separation between plates is \(d\) and potential difference \(V\) is applied between the plates. The force of attraction between the plates of the parallel plate air capacitor is:
| 1. | \(\frac{C^2V^2}{2d}\) | 2. | \(\frac{CV^2}{2d}\) |
| 3. | \(\frac{CV^2}{d}\) | 4. | \(\frac{C^2V^2}{2d^2}\) |
A parallel plate air capacitor of capacitance \(C\) is connected to a cell of emf \(V\) and then disconnected from it. A dielectric slab of dielectric constant \(K,\) which can just fill the air gap of the capacitor is now inserted in it. Which of the following is incorrect?
| 1. | The potential difference between the plates decreases \(K\) times. |
| 2. | The energy stored in the capacitor decreases \(K\) times. |
| 3. | The change in energy stored is \(\frac{1}{2}CV^{2}\left ( \frac{1}{K} -1\right )\) |
| 4. | The charge on the capacitor is not conserved. |
Two thin dielectric slabs of dielectric constants \(K_1\) and \(K_2\) \((K_1<K_2)\) are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field \('E'\) between the plates with distance \('d'\) as measured from the plate \(P\) is correctly shown by:

| 1. |  |
2. |  |
| 3. |  |
4. |  |








