The air density at Mount Everest is less than that at the sea level. It is found by mountaineers that for one trip lasting a few hours, the extra oxygen needed by them corresponds to 30,000 cc at sea level (pressure 1 atmosphere, temperature 27°C). Assuming that the temperature around Mount Everest is –73°C and that the oxygen cylinder has capacity of 5.2 litre, the pressure at which ${\mathrm{O}}_2$ be filled (at site) in cylinder is

1.  3.86 atm                     

2.  5.00 atm

3.  5.77 atm                     

4.  1 atm

$\frac{1}{2}$ mole of helium gas is contained in a container at S.T.P. The heat energy needed to double the pressure of the gas, keeping the volume constant (specific heat of the gas $=3 \mathrm{J} {\mathrm{gm}}^{-1} {\mathrm{K}}^{-1}$) is 

1.  3276 J                   

2.  1638 J

3.  819 J                     

4.  409.5 J

The equation of state of a gas is given by $\left(\mathrm{P}+\frac{{\mathrm{aT}}^2}{\mathrm{V}}\right){\mathrm{V}}^{\mathrm{c}}=\left(\mathrm{RT}+\mathrm{b}\right),$ where a, b, c and R are constants. The isotherms can be represented by $\mathrm{P}={\mathrm{AV}}^{\mathrm{m}}-{\mathrm{BV}}^{\mathrm{n}},$ where A and B depend only on temperature and 

1. $\mathrm{m}=-\mathrm{c} \mathrm{and} \mathrm{n}=-1$                       

2. $\mathrm{m}=\mathrm{c} \mathrm{and} \mathrm{n}=1$

3. $\mathrm{m}=-\mathrm{c} \mathrm{and} \mathrm{n}=1$                           

4. $\mathrm{m}=\mathrm{c} \mathrm{and} \mathrm{n}=-1$

\(70\) calories of heat is required to raise the temperature of \(2\) moles of an ideal gas at constant pressure from \(30^{\circ}\text{C}\) to \(35^{\circ}\text{C}\). The amount of heat required to raise the temperature of same gas through the same range \((30^{\circ}\text{C}~\text{to}~35^{\circ}\text{C})\) at constant volume (\(R=2\) cal/mol/K)
1. \(30\) cal
2. \(50\) cal
3. \(70\) cal
4. \(90\) cal

A closed compartment containing gas is moving with some acceleration in horizontal direction. Neglect effect of gravity. Then the pressure in the compartment is

1. Same everywhere                           

2. Lower in the front side

3. Lower in the rear side                     

4. Lower in the upper side

Three closed vessels A, B and C are at the same temperature T and contain gases which obey the Maxwellian distribution of velocities. Vessel A contains only ${\mathrm{O}}_2 , \mathrm{B}$ only ${\mathrm{N}}_2$ and C a mixture of equal quantities of ${\mathrm{O}}_2$ and ${\mathrm{N}}_2$. If the average speed of the ${\mathrm{O}}_2$ molecules in vessel A is ${\mathrm{V}}_1 ,$ that of the ${\mathrm{N}}_2$ molecules in vessel B is ${\mathrm{V}}_2 ,$ the average speed of the ${\mathrm{O}}_2$ molecules in vessel C is

1. $\left({\mathrm{V}}_1+{\mathrm{V}}_2\right)/2$                           

2. ${\mathrm{V}}_1$

3. ${\left({\mathrm{V}}_1{\mathrm{V}}_2\right)}^{1/2}$                               

4. $\sqrt{3 \mathrm{kT}/\mathrm{M}}$

A box containing N molecules of a perfect gas at temperature ${\mathrm{T}}_1$ and pressure ${\mathrm{P}}_1$. The number of molecules in the box is doubled keeping the total kinetic energy of the gas same as before. If the new pressure is ${\mathrm{P}}_2$ and temperature ${\mathrm{T}}_2$, then

1. ${\mathrm{P}}_2={\mathrm{P}}_1, {\mathrm{T}}_2={\mathrm{T}}_1$                           

2. ${\mathrm{P}}_2={\mathrm{P}}_1, {\mathrm{T}}_2=\frac{{\mathrm{T}}_1}{2}$

3. ${\mathrm{P}}_2=2{\mathrm{P}}_1, {\mathrm{T}}_2={\mathrm{T}}_1$                         

4. ${\mathrm{P}}_2=2{\mathrm{P}}_1, {\mathrm{T}}_2=\frac{{\mathrm{T}}_1}{2}$

Two identical glass bulbs are interconnected by a thin glass tube. A gas is filled in these bulbs at N.T.P. If one bulb is placed in ice and another bulb is placed in hot bath, then the pressure of the gas becomes 1.5 times. The temperature of hot bath will be

1.  100°C                     

2.  182°C

3.  256°C                     

4.  546°C

Two containers of equal volumes contain the same gas at pressures \(P_1\)${\mathrm{}}_{}$ and \(P_2\) and absolute temperatures \(T_1\) and \(T_2\), respectively. On joining the vessels, the gas reaches a common pressure \(P\) and common temperature \(T\). The ratio \(\dfrac{P}{T}\) is equal to:

At the top of a mountain, a thermometer reads \(7^\circ \text{C}\) and a barometer reads \(70\) cm of mercury. At the bottom of the mountain, the thermometer reads \(27^\circ \text{C},\) and the barometer reads \(76\) cm of mercury.

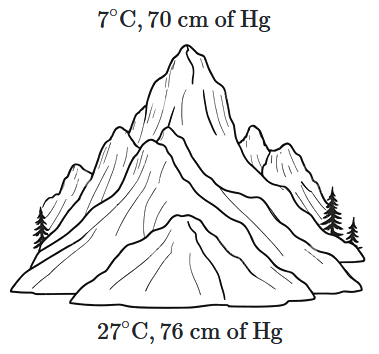
What is the comparison (ratio) of the air density at the top of the mountain to that at the bottom?