The wire shown in figure carries a current of 32 A. If r =3.14 cm, the magnetic field at point P will be
 1. 1.6×10-4T
1. 1.6×10-4T

| 1. | \({1 \over 499}G\) | 2. | \({499 \over 500}G\) |
| 3. | \({1 \over 500}G\) | 4. | \({500 \over 499}G\) |
| 1. | can be in equilibrium in one orientation |
| 2. | can be in equilibrium in two orientations, both the equilibrium states are unstable |
| 3. | can be in equilibrium in two orientations, one stable while the other is unstable |
| 4. | experiences a torque whether the field is uniform or non-uniform in all orientations |
A very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity , as shown, the force on the charge is-
1. Along OX
2. Opposite to OY
3. Along OY
4. Opposite to OX
A uniform electric field and a uniform magnetic field are acting in the same direction in a certain region. If an electron is projected in the region such that its velocity is pointed along the direction of fields, then the electron:
| 1. | speed will decrease |
| 2. | speed will increase |
| 3. | will turn towards the left of the direction of motion |
| 4. | will turn towards the right of the direction of motion |
Two charged particles having charges q and mass m are moving on circular paths in same uniform magnetic field with speed v and 2v. Ratio of their angular velocities are
1.
2.
3.
4.
A circular current-carrying coil has a radius \(R.\) The distance from the centre of the coil, on the axis, where \(B\) will be \(\frac18\) of its value at the centre of the coil is:
1. \(\frac{R}{\sqrt3}\)
2. \(\sqrt3R\)
3. \(2\sqrt3R\)
4. \(\frac{2R}{\sqrt3}\)
1. 1 A
2. 58 A
3. 58 mA
4. 30 mA
| 1. | Angle between \(\vec v\) and \(\vec {B}\) is necessarily \(90^{\circ}\). |
| 2. | Angle between \(\vec v\) and \(\vec {B}\) can have any value other than \(90^{\circ}\). |
| 3. | Angle between \(\vec v\) and \(\vec {B}\) can have any value other than zero and \(180^{\circ}\). |
| 4. | Angle between \(\vec v\) and \(\vec {B}\) is either zero or \(180^{\circ}\). |
Magnetic field at point O will be: (assume straight wire segments are infinite)
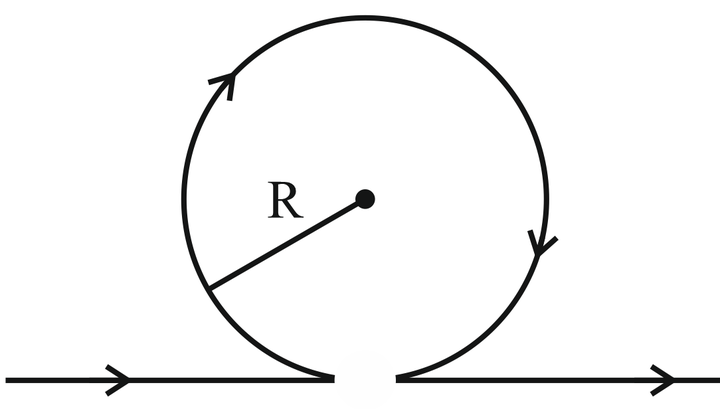
1. \(\frac{\mu_{_0}l}{2R}\) interior
2. \(\frac{\mu_{_0}l}{2R}\) exterior
3. \(\frac{\mu_{_0}l}{2R}1-\frac{l}{\pi}\) interior
4. \(\frac{\mu_{_0}l}{2R}1-\frac{l}{\pi}\) exterior







