As shown in the figure, P and Q are two coaxial conducting loops separated by some distance. When the switch S is closed, a clockwise current I_P flows in P (as seen by E) and an induced current $I_{Q_1}$ flows in Q. The switch remains closed for a long time. When S is opened, a current $I_{Q_2}$ flows in Q. Then the directions of $I_{Q_1}$ and $I_{Q_2}$ (as seen by E) are 

(1) Respectively clockwise and anticlockwise

(2) Both clockwise

(3) Both anticlockwise

(4) Respectively anticlockwise and clockwise

A conducting wireframe is placed in a magnetic field that is directed into the paper. The magnetic field is increasing at a constant rate. The directions of induced current in wires AB and CD are

(1) B to A and D to C

(2) A to B and C to D

(3) A to B and D to C

(4) B to A and C to D

A conductor ABOCD moves along its bisector with a velocity of \(1\) m/s through a perpendicular magnetic field of \(1~\text{wb/m}^2\), as shown in fig. If all the four sides are of \(1\) m length each, then the induced emf between points A and D is:
                  
1. \(0\)

2. \(1.41\) volt

3. \(0.71\) volt

4. None of the above

A conducting rod PQ of length L = 1.0 m is moving with a uniform speed v = 2 m/s in a uniform magnetic field B = 4.0 T directed into the paper. A capacitor of capacity C = 10 μF is connected as shown in figure. Then

(1) q_A = + 80 μC and q_B = – 80 μC

(2) q_A = – 80 μC and q_B = + 80 μC

(3) q_A = 0 = q_B

(4) Charge stored in the capacitor increases exponentially with time

The resistance in the following circuit is increased at a particular instant. At this instant the value of resistance is 10Ω. The current in the circuit will be now

(1) i = 0.5 A

(2) i > 0.5 A

(3) i < 0.5 A

(4) i = 0

A highly conducting ring of radius R is perpendicular to and concentric with the axis of a long solenoid as shown in fig. The ring has a narrow gap of width d in its circumference. The solenoid has a cross-sectional area A and a uniform internal field of magnitude B₀. Now beginning at t = 0, the solenoid current is steadily increased so that the field magnitude at any time t is given by B(t) = B₀ + αt where α > 0. Assuming that no charge can flow across the gap, the end of the ring which has an excess of positive charge and the magnitude of induced e.m.f. in the ring are respectively

(1) X, Aα

(2) X πR²α

(3) Y, πA²α

(4) Y, πR²α

A wire cd of length \(l\) and mass \(m\) is sliding without friction on conducting rails \(ax\) and \(by\) as shown. The vertical rails are connected to each other with a resistance \(R\) between \(a\) and \(b\). A uniform magnetic field \(B\) is applied perpendicular to the plane \(abcd\) such that \(cd\) moves with a constant velocity of:

A conducting rod \(AC\) of length \(4l\) is rotated about point \(O\) in a uniform magnetic field \(\vec {B}\) directed into the paper. If \(AO = l\) and \(OC = 3l\), then:

   
1. \(V_{A} - V_{O} = \dfrac{B \omega l^{2}}{2}\)
2. \(V_{O} - V_{C} = \dfrac{7}{2} B \omega l^{2}\)
3. \(V_{A} - V_{C} = 4 B \omega l^{2}\)
4. \(V_{C} - V_{O} = \dfrac{9}{2} B \omega l^{2}\)

The network shown in the figure is a part of a complete circuit. If at a certain instant the current i is 5 A and is decreasing at the rate of 10³ A/s then V_B – V_A is

(1) 5 V

(2) 10 V

(3) 15 V

(4) 20 V

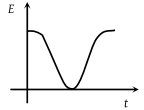
The variation of induced emf (E) with time (t) in a coil if a short bar magnet is moved along its axis with a constant velocity is best represented as

(1)

(2)

(3)

(4)