The bob of a pendulum of length l is pulled aside from its equilibrium position through an angle $\theta$ and then released. The bob will then pass through its equilibrium position with a speed v, where v equals

(1) $\sqrt{2\mathrm{gl}(1-\mathrm{sin\theta })}$

(2) $\sqrt{2\mathrm{gl}(1+\mathrm{cos\theta })}$

(3) $\sqrt{2\mathrm{gl}(1-\mathrm{cos\theta })}$

(4) $\sqrt{2\mathrm{gl}(1+\mathrm{sin\theta })}$

A spring 40 mm long is stretched by the application of force. If 10 N force is required to stretch the spring through 1 mm, then work done to stretch the spring 40 mm is equal to:

Two springs with spring constants $k_1$ = 1500 N/m and $k_2$ = 3000 N/m are stretched by the same force. The ratio of potential energy stored in the springs will be 

1. 2:1

2. 1:2

3. 4:1

4. 1:4

A block of mass \(2~\text{kg}\) moving with a velocity of \(10~\text{m/s}\) on a smooth surface hits a spring of force constant \(80\times10^3~\text{N/m}\) as shown in the figure. The maximum compression in the spring will be:
               
1. \(5~\text{cm}\) 
2. \(10~\text{cm}\)
3. \(15~\text{cm}\)
4. \(20~\text{cm}\)

A particle of mass 10 kg is moving with velocity of $10\sqrt{x}$ m/s, where x is displacement . The work done by net force during the displacement of particle form x = 4 to x = 9 m is 

1. 1250 J

2. 1000 J

3. 3500 J

4. 2500 J

The relation between velocity (v) and time (t) is $\mathrm{v\alpha }\sqrt{\mathrm{t}}$, then which one of the following quantity is constant:

1.  Force

2.  Power

3.  Momentum

4.  Kinetic Energy

A particle is moving on the circular path of the radius (R) with centripetal acceleration $a_c=k^{2}R{t}^2$. Then the correct relation showing power (P) delivered by net force versus time (t) is 

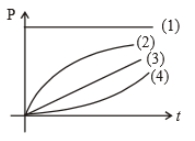
1. 1

2. 2

3. 3

4. 4

A force F is applied on a body which moves with a velocity v in the direction of the force, then the power will be

1.  ${\mathrm{Fv}}^2$

2.  Fv

3.  $\mathrm{F}/{\mathrm{v}}^2$

4.  F/v

A mass m slips along the wall of a semispherical surface of radius R. The velocity at the bottom of the surface is [ MP PMT 1993]

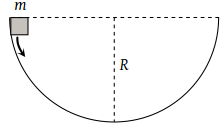
(1) $\sqrt{Rg}$

(2) $\sqrt{2Rg}$

(3) $2\sqrt{\pi Rg}$

(4) $\sqrt{\pi Rg}$