The angle made by the vector $\overrightarrow{\mathrm{A}} = \sqrt{3}\hat{\mathrm{i}} + 3\hat{\mathrm{j}} + 2\hat{\mathrm{k}}$ with y-axis is:

1.  ${\sin }^{-1}\left(\frac{3}{\sqrt{14}}\right)$

2.  ${\sin }^{-1}\left(\frac{\sqrt{7}}{4}\right)$

3.  ${\cos }^{-1}\left(\frac{4}{3}\right)$

4.  ${\cos }^{-1}\left(\frac{3}{5}\right)$

In the space, if the sum of vectors of unequal magnitude is zero, then the minimum number of vectors are:
1. \(2\)
2. \(3\)
3. \(4\)
4. \(5\)

If $\overrightarrow{\mathrm{A}} + \overrightarrow{\mathrm{B}}$ is perpendicular to $\overrightarrow{\mathrm{A}} - \overrightarrow{\mathrm{B}}$  , then which of the following statement is correct?

1. $\left|\overrightarrow{\mathrm{A}}\right| = \left|\overrightarrow{\mathrm{B}}\right|$

2. $\overrightarrow{\mathrm{A}} \perp \overrightarrow{\mathrm{B}}$

3. $\overrightarrow{\mathrm{A}}·\overrightarrow{\mathrm{B}} = \mathrm{zero}$

4. $\left(\overrightarrow{\mathrm{A}} + \overrightarrow{\mathrm{B}}\right)·\left(\overrightarrow{\mathrm{A}} - \overrightarrow{\mathrm{B}}\right) \ne 0$

The angle between the two vectors \(\left(- 2 \hat{i} +3 \hat{j} + \hat{k}\right)\) and \(\left(\hat{i} + 2 \hat{j} - 4 \hat{k}\right)\) is:
1. \(0^{\circ}\)
2. \(90^{\circ}\)
3. \(180^{\circ}\)
4. \(45^{\circ}\)

If $\overrightarrow{\mathrm{a}} + \overrightarrow{\mathrm{b}} + \overrightarrow{\mathrm{c}} = \overrightarrow{0}$; then which of the following statements is incorrect?

(1) $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}} \mathrm{and} \overrightarrow{\mathrm{c}}$ must each be a null vector.

(2) The magnitude of $\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}$ equals the magnitude of $\overrightarrow{\mathrm{c}}$.

(3) The magnitude of ä can never be greater than the sum of the magnitudes of $\overrightarrow{\mathrm{b}}$ and $\overrightarrow{\mathrm{c}}$

(4) ä must lie in the plane of $\overrightarrow{\mathrm{b}}$ and $\overrightarrow{\mathrm{c}}$.

When a force of magnitude F acts on a body of mass m the acceleration produced in the body is a. If three coplanar forces of equal magnitude F act on the same body as shown in the figure, then acceleration produced is

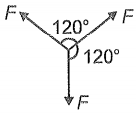
1.  0

2.  $\left(\sqrt{3} +\hspace{0.17em}1\right)\mathrm{a}$

3.  $\left(\sqrt{3} -\hspace{0.17em}1\right)\mathrm{a}$

4.  $\sqrt{3}\mathrm{a}$

Three forces each of magnitude 1 N act along with the sides AB, BC, and CD of a regular hexagon. The magnitude of their resultant is:

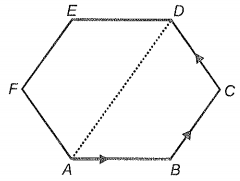
(1) 4N 

(2) Zero

(3) 2 N

(4) 1 N

If a unit vector \(\hat j\) is rotated through an angle of \(45^{\circ}\) anticlockwise, then the new vector will be:
1. \(\sqrt{2}\hat i + \sqrt{2}\hat j\)
2. \(\hat i + \hat j\)
3. \(\frac{1}{\sqrt{2}}\hat i + \frac{1}{\sqrt{2}}\hat j\)
4. \(-\frac{1}{\sqrt{2}}\hat i + \frac{1}{\sqrt{2}}\hat j\)

If $\overrightarrow{\mathrm{a}} = 2\hat{\mathrm{i}} + \hat{\mathrm{j}}$ and $\overrightarrow{\mathrm{b}} = 3\hat{\mathrm{i}} + 2\hat{\mathrm{j}}$, then $\left|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}\right|=?$ 

$\stackrel{}{\mathrm{}}$\(\overrightarrow A\) and \(\overrightarrow {B}\) are two vectors given by \(\overrightarrow {A}= 2\hat i + 3\hat j\) and \(\overrightarrow {B}= \hat i + \hat j\). The component of \(\overrightarrow A\) parallel to \(\overrightarrow B\) is:
1. \(\frac{(2\hat i -\hat j)}{2}\)
2. \(\frac{5}{2}(\hat i - \hat j)\)
3. \(\frac{5}{2}(\hat i + \hat j)\)
4. \(\frac{(3\hat i -2\hat j)}{2}\)