Three identical spheres, each of mass \(M\), are placed at the corners of a right-angle triangle with mutually perpendicular sides equal to \(2~\text{m}\) (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of the centre of mass.

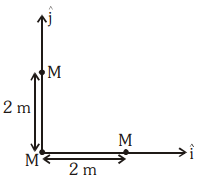
1.	\(2( \hat{i}+ \hat{j})\)	2.	\(( \hat{i}+ \hat{j})\)
3.	\({2 \over 3}( \hat{i}+ \hat{j})\)	4.	\({4 \over 3}( \hat{i}+ \hat{j})\)

What would be the torque about the origin when a force \(3\hat{j}~\text N\) acts on a particle whose position vector is \(2\hat{k}~\text m?\)

Two particles of mass \(5~\text{kg}\) and \(10~\text{kg}\) respectively are attached to the two ends of a rigid rod of length \(1~\text{m}\) with negligible mass. The centre of mass of the system from the \(5~\text{kg}\) particle is nearly at a distance of:
1. \(50~\text{cm}\)
2. \(67~\text{cm}\)
3. \(80~\text{cm}\)
4. \(33~\text{cm}\)

A uniform square plate \(ABCD\) has a mass of \(10\) kg. If two point masses of \(5\) kg each are placed at the corners \(C\) and \(D\) as shown in the adjoining figure, then the centre of mass shifts to the mid-point of:
            
1. \(OH\)

2. \(DH\)

3. \(OG\)

4. \(OF\) 

The mass per unit length of a non-uniform rod of length \(L\) is given by \(\mu =λx^{2}\) where \(\lambda\) is a constant and \(x\) is the distance from one end of the rod. The distance between the centre of mass of the rod and this end is:

The law of conservation of angular momentum is valid when:

The angular speed of the wheel of a vehicle is increased from \(360~\text{rpm}\) to \(1200~\text{rpm}\) in \(14\) seconds. Its angular acceleration will be:
1. \(2\pi ~\text{rad/s}^2\)
2. \(28\pi ~\text{rad/s}^2\)
3. \(120\pi ~\text{rad/s}^2\)
4. \(1 ~\text{rad/s}^2\)

Three identical spheres, each of mass \(M\), are placed at the corners of a right-angle triangle with mutually perpendicular sides equal to \(2~\text{m}\) (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of the centre of mass. 
        
1. \(2(\hat{i}+\hat{j})\)
2. \(\hat{i}+\hat{j}\)
3. \(\frac{2}{3}(\hat{i}+\hat{j})\)
4. \(\frac{4}{3}(\hat{i}+\hat{j})\)

In the three figures, each wire has a mass M, radius R and a uniform mass distribution. If they form part of a circle of radius R, then about an axis perpendicular to the plane and passing through the centre (shown by crosses), their moment of inertia is in the order:

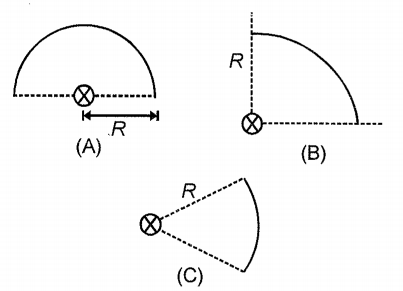
1.  $I_A$ $>$ $I_B$ $>$ $$ $I_C$

2.  $I_A$ $=$ $I_B$ $=$ $I_C$

3.  $I_A$ $<$ $I_B$ $<$ $I_C$

4.  $I_A$ $<$ $I_C$ $<$ $I_B$