A beam of light from a source \(L\) is incident normally on a plane mirror fixed at a certain distance \(x\) from the source. The beam is reflected back as a spot on a scale placed just above the source \(L.\) When the mirror is rotated through a small angle \(\theta,\) the spot of the light is found to move through a distance \(y\) on the scale. The angle \(\theta\) is given by:
1.
\(\dfrac{y}{x}\)
2.
\(\dfrac{x}{2y}\)
3.
\(\dfrac{x}{y}\)
4.
\(\dfrac{y}{2x}\)
A thin prism having refracting angle \(10^\circ\) is made of glass of a refractive index \(1.42\). This prism is combined with another thin prism of glass with a refractive index \(1.7\). This combination produces dispersion without deviation. The refracting angle of the second prism should be:
1. \(6^{\circ}\)
2. \(8^{\circ}\)
3. \(10^{\circ}\)
4. \(4^{\circ}\)
An air bubble in a glass slab with a refractive index \(1.5\) (near-normal incidence) is \(5~\text{cm}\) deep when viewed from one surface and \(3~\text{cm}\) deep when viewed from the opposite surface. The thickness (in \(\text{cm}\)) of the slab is:
| 1. | \(8\) | 2. | \(10\) |
| 3. | \(12\) | 4. | \(16\) |
A person can see objects clearly only when they lie between \(50\) cm and \(400\) cm from his eyes. In order to increase the maximum distance of distinct vision to infinity, the type and power of the correcting lens, the person has to use, will be:
| 1. | convex, \(+2.25\) D | 2. | concave, \(-0.25\) D |
| 3. | concave, \(-0.2\) D | 4. | convex, \(+0.5\) D |
An astronomical refracting telescope will have large angular magnification and high angular resolution when it has an objective lens of:
| 1. | small focal length and large diameter. |
| 2. | large focal length and small diameter. |
| 3. | large focal length and large diameter. |
| 4. | small focal length and small diameter. |
| 1. | \(46.0\text{cm}\) | 2. | \(50.0\text{cm}\) |
| 3. | \(54.0\text{cm}\) | 4. | \(37.3\text{cm}\) |
(Where \(m\) is the magnification produced by the mirror)
| Column-I | Column-II | ||
| A. | \(m= -2\) | I. | convex mirror |
| B. | \(m= -\frac{1}{2}\) | II. | concave mirror |
| C. | \(m= +2\) | III. | real Image |
| D. | \(m= +\frac{1}{2}\) | IV. | virtual Image |
Codes:
| A | B | C | D | |
| 1. | I & III | I & IV | I & II | III & IV |
| 2. | I & IV | II & III | II & IV | II & III |
| 3. | III & IV | II & IV | II & III | I & IV |
| 4. | II & III | II & III | II & IV | I & IV |
| 1. | \(45^{0},~\sqrt{2}\) | 2. | \(30^{0},~\sqrt{2}\) |
| 3. | \(30^{0},~\frac{1}{\sqrt{2}}\) | 4. | \(45^{0},~\frac{1}{\sqrt{2}}\) |
In an astronomical telescope in normal adjustment, a straight line of length \(L\) is drawn on the inside part of the objective lens. The eye-piece forms a real image of this line. The length of this image is \(l.\) The magnification of the telescope is:
1. \(\frac{L}{l}+1\)
2. \(\frac{L}{l}-1\)
3. \(\frac{L+1}{l-1}\)
4. \(\frac{L}{l}\)
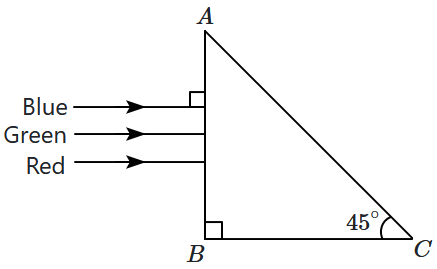
The prism will:
| 1. | separate the blue colour part from the red and green colour. |
| 2. | separate all three colours from one another. |
| 3. | not separate the three colours at all. |
| 4. | separate the red colour part from the green and blue colours. |






