The coefficient of performance of a refrigerator is \(5.\) If the temperature inside the freezer is \(-20^\circ \text{C},\) the temperature of the surroundings to which it rejects heat is:
1. \(31^\circ \text{C}\)
2. \(41^\circ \text{C}\)
3. \(11^\circ \text{C}\)
4. \(21^\circ \text{C}\)

The figure below shows two paths that may be taken by gas to go from state \(A\) to state \(C.\) 
                    
In process \(AB,\) \(400~\text{J}\) of heat is added to the system, and in process \(BC,\)  \(100~\text{J}\) of heat is added to the system. The heat absorbed by the system in the process \(AC\) will be:
1. \(380~\text{J}\)
2. \(500~\text{J}\)
3. \(460~\text{J}\)
4. \(300~\text{J}\)

A Carnot engine, having an efficiency of $\mathrm{\eta }$ = $\frac{1}{10}$ as a heat engine, is used as a refrigerator. If the work done on the system is \(10\) J, the amount of energy absorbed from the reservoir at a lower temperature is:
1. \(100\) J
2. \(99\) J
3. \(90\) J
4. \(1\) J

A thermodynamic system undergoes a cyclic process \(ABCDA\) as shown in Fig. The work done by the system in the cycle is: 
             
1. \( P_0 V_0 \)
2. \( 2 P_0 V_0 \)
3. \( \frac{P_0 V_0}{2} \)
4. zero

A thermodynamic system is taken through the cycle \(ABCD\) as shown in the figure. Heat rejected by the gas during the cycle is: 
      

1. \(2 {PV}\)
2. \(4{PV}\)
3. \(\frac{1}{2}{PV}\)
4. \(PV\)

One mole of an ideal gas goes from an initial state \(A\) to the final state \(B\) with two processes. It first undergoes isothermal expansion from volume \(V\) to \(3V\) and then its volume is reduced from \(3V\) to \(V\) at constant pressure. The correct \((P-V)\) diagram representing the two processes is:

1.		2.
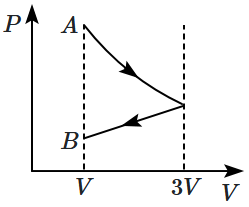3.		4.